【初心者向けR】医学研究でよく出る「リスク比」「オッズ比」を『epiR』を用いて実戦形式で解説！

2025年5月24日

URLをコピーしました！

こんにちは。ほしのはやしです。

今回は、医学研究や論文でよく見る「リスク比（RR）」「オッズ比（OR）」を実際のデータを用いて、どのようにデータを変形し解析するかを初心者向けにやさしく解説していきます。

リスク比・オッズ比の概略は下記ページを参考にしてください！

データの準備（例：ワクチンと感染）

必須パッケージである『tidyverse』と『epiR』をインストールしておいてください。

# パッケージの読み込み
library(tidyverse)
library(epiR)

# 仮のデータ作成
df <- tibble(
  patient_id = 1:100,
  vaccine = sample(c("Yes", "No"), 100, replace = TRUE),
  infected = sample(c("Yes", "No"), 100, replace = TRUE, prob = c(0.2, 0.8))
)

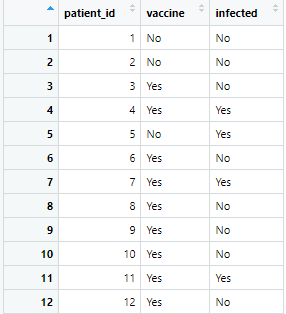
この架空のデータセットを2×2の表に以下の原則に従って変更していきます。

【2×2表の原則】
行方向（縦）：
- 行1：介入あり（たとえばワクチン接種あり）
- 行2：介入なし（たとえばワクチン接種なし）

列方向（横）：
- 列1：標的となる結果（たとえば「感染あり」など）
- 列2：標的以外の結果（たとえば「感染なし」など）

# 2×2表を作成（行：vaccine Yes/No、列：infected Yes/No）
table_rr <- df %>%
  count(vaccine, infected) %>%
  pivot_wider(names_from = infected, values_from = n, values_fill = 0) %>%
  arrange(factor(vaccine, levels = c("Yes", "No"))) %>%
  select(Yes, No) %>%
  as.matrix()

# リスク比を計算
epi.2by2(table_rr, method = "cohort.count", conf.level = 0.95)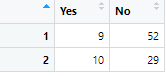

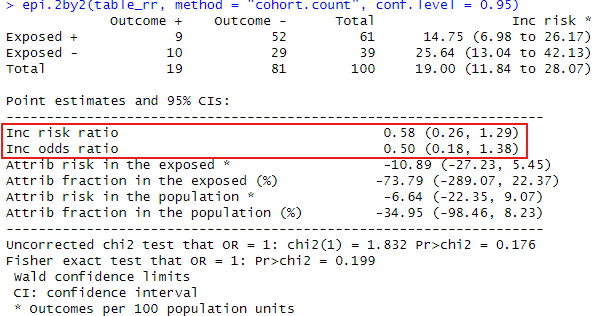
このようにリスク比とオッズ比を得ることができました！

コードの解説

  count(vaccine, infected) %>%

この部分で、ワクチン接種（vaccine）と感染（infected）の組み合わせごとに人数を数えます。

ここまでで表が以下のように成型されます。

vaccine	infected	n
Yes	Yes	9
Yes	No	52
No	Yes	10
No	No	29

  pivot_wider(names_from = infected, values_from = n, values_fill = 0) %>%

pivot_widerは縦型の列を横型に変形する関数です。
詳しくは下記ページを参考にしてください。

vaccine	Yes（感染した）	No（感染しなかった）
Yes	9	52
No	10	29

結果の読み方・解釈

以下の結果の読み方について解説していきます！

表の上の部分の説明

	感染した（Outcome +）	感染しなかった（Outcome -）	合計人数（Total）	感染リスク（Inc risk *）
ワクチン接種者（Exposed +）	9人	52人	61人	14.75%（95%CI: 7.0–26.2%）
非接種者（Exposed -）	10人	29人	39人	25.64%（95%CI: 13.0–42.1%）
全体（Total）	19人	81人	100人	19.00%（95%CI: 11.8–28.1%）

Inc risk は「100人あたり何人が感染したか（＝感染リスク）」を示しています。
ワクチンを打った人のほうが感染しにくそうに見えます（14.75% vs 25.64%）。

表の真ん中の説明

指標	説明	結果（95%信頼区間）	意味
Inc risk ratio（リスク比）	ワクチンを打った人の感染リスク ÷ 打ってない人の感染リスク	0.58 (0.26–1.29)	1より小さい → ワクチンにより感染が減る傾向（でも有意差なし）
Inc odds ratio（オッズ比）	感染する「可能性の比」	0.50 (0.18–1.38)	同様に、感染が減る傾向あり（でも不確か）
Attrib risk in the exposed（接種群の差分リスク）	ワクチンが減らした感染率	−10.89（−27.2～+5.5）	ワクチンを打ったことで、感染が10.9%減ったかもしれない（でも不確実）
Attrib fraction in exposed (%)（ワクチンでどれくらい防げたか）	接種者内の感染のうち、ワクチンが防いだ割合	−73.79%（非常に不確実）	値が不安定で信頼区間が広く、確かな効果は言えない
Attrib risk in the population	ワクチンによる全体の感染減少	−6.64（−22.35～+9.07）	社会全体で見たワクチンの効果（でも有意差なし）