こんにちは。ほしのはやしです。
次元削減(Dimensionality Reduction)は、機械学習や統計解析において重要な手法の一つです。
でも、「次元って何?」「なぜ減らすの?」と疑問に思う方もいらっしゃいますよね。
このページでは、次元削減の考え方とRを使った実践方法をわかりやすく解説します!
次元削減とは?
次元とは、分析に使う変数の数を意味します。
例えば、「身長・体重・年齢・血圧」など4つの変数を持つデータは、4次元のデータです。
でも、変数が多すぎると、
- ノイズが増える
- 可視化が難しい
- モデルが過学習しやすくなる
などの問題が発生します。
そこで、「情報をなるべく保ったまま、変数を減らす」ための技術が次元削減です。
次元削減はどんな場面で使うの?
- 遺伝子発現データ:数万個の遺伝子から重要なものだけを抽出
- 画像データ解析:画素(ピクセル)が数千~数万個
- マーケティング:多項目のアンケート結果を要約して傾向を把握
- クラスタリングや分類:特徴量が多すぎると精度が落ちるため、前処理として使用
このような大規模データに対して、データの外観をつかんで新たな着想を得たり、解析に適した形にすることを目的としてきます。
今回は、最も基本的な主成分分析について解説していきます!
主成分分析(PCA)を使って次元削減してみよう
PCAの寄与率(Proportion of Variance)の評価
次元削減を達成するために、まずは主成分分析について説明していきます。
Rに内蔵されている irisデータセットを使って、実際にPCAを試してみましょう。
# データの確認
head(iris)
# 数値データだけを抽出(Speciesは因子なので除外)
iris_data <- iris[, 1:4]
# 主成分分析(PCA)を実行
pca_result <- prcomp(iris_data, scale. = TRUE)
# 結果を確認
summary(pca_result)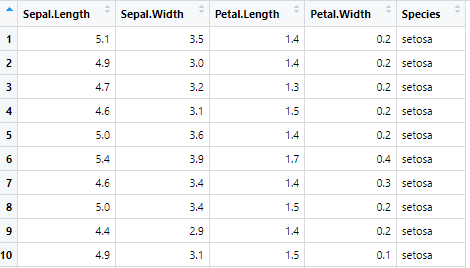
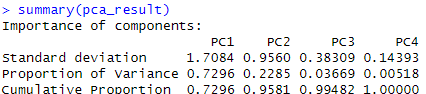
主成分分析では、まずこのように、元のデータとは別のPC1, PC2, PC3, PC4などという新しい評価軸を作成することから始まります。
このPCという軸を使ってデータをどれだけ説明できるか、を表したのが『Proportion of Variance』です。
『Cumulative proportion』は『Proportion of Variance』の累積の割合ですね!
「Proportion of Variance」が高い主成分ほど重要
累積寄与率(Cumulative Proportion)が80%以上になるところまでを使うのが一般的
今回の結果では、PC1が72.96%、PC2までで累計95.81%なので、PC1、PC2でほぼデータを説明できるということがわかります!
PCAの負荷量(Loadings)の評価
続いて、各主成分が元の変数のどの組み合わせ(線形結合)で構成されているか、が気になってくると思います。
これを表したものが負荷量といいます。
pca_result$rotation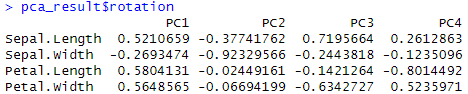
PCA分析で得た結果のデータ名$rotation で負荷量を確認することができます!
・数値の絶対値が大きい変数ほど、その主成分に強く影響
・負の値でも意味あり(向きが逆)
PC1では、Petal.Length (0.580), Petal.Width (0.565), Sepal.Length (0.521) が高い
⇒ PC1は「花びらの大きさ・がくの長さ」に関連する成分と考えられます。
PC2では、Sepal.Width (-0.923) のみ割合が大きい
⇒ PC2は「がくの幅」に特化した成分だとわかります。
これでどんな組み合わせの集団が良さそうかイメージがついてきました!
PCAを可視化する
最後に、PC1、PC2の軸でデータを新しく可視化してみましょう!
# ggplot2を使って主成分をプロット
library(ggplot2)
# 主成分スコアのデータフレームを作成
pca_df <- as.data.frame(pca_result$x)
pca_df$Species <- iris$Species
# PC1とPC2でプロット
ggplot(pca_df, aes(x = PC1, y = PC2, color = Species)) +
geom_point(size = 2) +
labs(title = "PCAによる次元削減と可視化") +
theme_classic()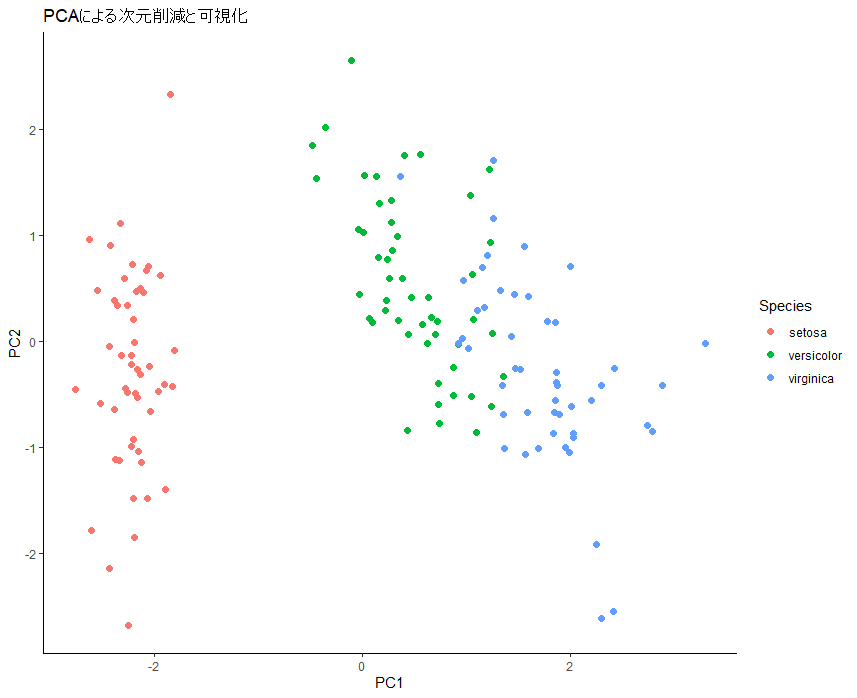
このグラフを見ると、横軸でグループ(Speciesの色分け)がきれいにわかれてそうですね!
すなわち、PC1が分類に効果ありそう!ということがわかります!!
もしグラフが対角線上に並んでいれば、PC1, PC2のどちらも重要ということになりますね!
目的別に見る「PCAの次に行う解析」
これまでの結果をもとに、次に取るべき解析ステップは、目的に応じて以下のように分かれます。
① 分類が目的の場合(例:品種を当てたい、予測したい)
PCA+分類モデルの組み合わせへ進みます。
よく使う手法:
| 手法 | 説明 |
|---|---|
| ロジスティック回帰 | シンプルな分類モデル。2クラス or 多クラス分類に。 |
| ランダムフォレスト | 高精度・変数の重要度も出せる。解釈性あり。 |
| SVM(サポートベクターマシン) | 複雑な境界も対応できる。PCAと相性良い。 |
| k-NN(k近傍法) | PCAで次元を下げると効果的になることが多い。 |
PCAの主成分を使う理由:
- 元の高次元データよりも「ノイズが少なく、分類に効く軸」が抽出されている。
- すなわち、過学習を防ぎつつ、シンプルな分類モデルを構築できる。
② クラスタ構造の探索が目的の場合(教師なし学習)
クラスタリングを行います(教師なし学習の続きとして行うことが多いです)
よく使う手法:
| 手法 | 説明 |
|---|---|
| k-meansクラスタリング | PCAで次元削減後に使うとクラスタがきれいに分かれることが多い |
| 階層的クラスタリング(hclust) | デンドログラムで階層構造を見たいときに便利 |
| DBSCAN | ノイズや不均一な密度に強いクラスタリング手法 |
③ 変数の重要度や特徴量の選択が目的の場合
PCAの「負荷量(loadings)」を利用した解釈や、変数選択・特徴量設計に進みます。
具体的に行うこと:
- PC1に強く寄与している変数 → モデルに含めるべき重要特徴量
- PC1とPC2に寄与していない変数 → ノイズや不要な特徴かも?
応用:
- 回帰分析に使う変数の選別
- 可視化目的で特徴量を組み合わせる(例:新しい軸を定義)
④ 次元削減したデータで視覚的探索を続ける場合
- PCAスコアに基づき、さらに t-SNE や UMAP などの他の次元削減に進むこともあります。
- これは「より非線形な構造が隠れていそう」なときに使います。
 星柴くん
星柴くん次元削減と主成分分析について勉強したのだ!



ビッグデータ解析や症候群の新しい分類とか色んなことに使える基本テクニックなんやで!



漠然としたデータがわかりやすくなった!!
まとめ
次元削減と主成分分析について解説しました!
特に色んな変数をいっぱい集めて分類したり、見えにくいものを見やすくして新しく着想を得たり、非常に便利に使用することができます!
少しでも皆様のお役に立てたなら幸いです。










コメント