こんにちは。ほしのはやしです。
医学研究や疫学研究では、「この結果は前提が変わっても変わらないのか?」という疑問がよく出てきます。
そんなときに役立つのが感度分析(Sensitivity Analysis)です。
このページでは、感度分析とは何か、どんなときに使うのか、そしてRを使った簡単な実例について解説していきます!
感度分析とは?
感度分析とは、「ある前提条件やパラメータを変更したときに、結果がどれくらい変化するか」を検討する手法です。
目的は、『研究結果の頑健性(robustness)』を確かめることにあります。
例1:欠損データの影響を確認する
たとえば、ある疫学研究で「喫煙の有無」が重要な変数だとします。しかし、アンケートに答えなかった人が10%いて、その人たちの喫煙状況が不明です。
このとき、以下のような仮定で感度分析を行います:
- 欠測者を全員「非喫煙者」と仮定
- 欠測者を全員「喫煙者」と仮定
- 欠測者を「半分喫煙、半分非喫煙」と仮定
これらの条件下で解析をやり直し、結果が大きく変わらなければ、「喫煙の有無に関するデータの欠損があっても、結論は頑健である」と判断できます。
例2:交絡因子があるかもしれない
たとえば、ある薬剤が「血圧を下げる効果があるか?」を検証する研究において、食事や運動習慣の情報を取得していなかったとします。
ここでの感度分析は、「もし交絡因子(例えば塩分摂取)が強く影響していたら、結果はどう変わるか?」という仮定のもとに分析をします。
- 「交絡因子が薬と血圧の関係に与える影響」をシミュレーション
この上での解析でも、仮に強い影響があったとしても薬剤の効果が維持されれば、結論は比較的信頼できる、と判断できます。
例3:パラメータの仮定が正確でない場合
コスト効果分析などでよくあるのが、「医療費」や「治療効果の持続期間」などの数値が正確に分からないときです。
- 医療費が想定より20%高かったら?
- 効果が持続するのは1年ではなく半年だったら?
このように、さまざまな仮定のもとで試算を行い、最終的な結論(この治療は費用対効果があるか?)が変わるかどうかを確認します。
 星柴くん
星柴くん感度分析は、「もし○○だったらどうなる?」という仮定に基づく思考実験なんだね!



不確実なデータに対して柔軟に対応して信頼性を高めるためのテクニックとして便利やでな!
どんなときに使うの?
感度分析は先程の例をあげたように以下の場面で使われます。
・欠測データを補完したとき、補完方法によって結果が変わらないか確認したい
・潜在的な交絡因子(confounder)があるが、それがどの程度結果に影響するかを知りたい
・仮定したリスクモデルのパラメータが不確かである場合、その不確実性の影響を調べたい
Rで感度分析をしてみよう!
例題を以下のように考えます。
例1:薬剤Aの効果を検証する臨床試験
ある研究で、薬剤Aが心不全のリスクを減らすかどうかを調べたい。
交絡因子として糖尿病の有無が考えられたが、一部の患者に糖尿病の情報が欠けていました。
このとき、以下の2つの方法で感度分析を行います:
- 糖尿病が「ある」と仮定した場合
- 糖尿病が「ない」と仮定した場合
サンプルデータの作成
# パッケージの読み込み
library(tidyverse)
library(broom)
# データの準備
set.seed(123)
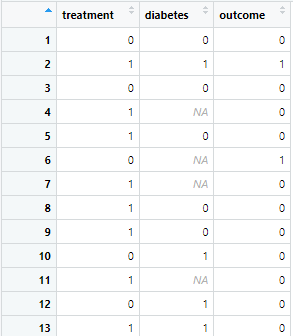
df <- tibble(
treatment = rbinom(100, 1, 0.5),
diabetes = sample(c(0, 1, NA), 100, replace = TRUE, prob = c(0.4, 0.4, 0.2)),
outcome = rbinom(100, 1, 0.3)
)

broom パッケージ
統計モデルの出力を整ったデータフレーム(tidy data)に変換してくれるパッケージです。tidyverse によるデータ処理や可視化と非常に相性が良く、分析後の処理がとてもスムーズになるのでおすすめ!!
欠損値を補完するパターンを作成
データにはNAがあるため、これを糖尿病なしとして補完するパターンと、糖尿病ありとして補完するパターンを作成します(パターンのリスト名『fill_patterns』)。
# 欠損値の補完パターンを作成
fill_patterns <- list(
"diabetes_0" = 0, # 欠損値を0(非糖尿病)として補完
"diabetes_1" = 1 # 欠損値を1(糖尿病)として補完
)各補完パターンで感度分析を実行
続いて、感度分析を実行します。
# 各補完パターンで感度分析を実行
results <- map_dfr(names(fill_patterns), function(name) {
filled_df <- df %>%
mutate(diabetes = if_else(is.na(diabetes), fill_patterns[[name]], diabetes))
model <- glm(outcome ~ treatment + diabetes, data = filled_df, family = binomial)
tidy(model) %>%
mutate(pattern = name)
})
View(results)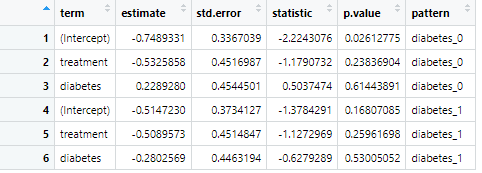

薬剤の効果(treatmentの行のestimate)が大きく変わらなければ、「結果は糖尿病情報の欠損に対して頑健」と判断できます。
感度分析のブレの大きさの目安
感度分析において「どの程度ズレたら結果が頑健でない」と判断するかに明確な絶対基準はありません。
ただし、以下の3つの観点から合理的に判断します。
| 判断基準 | 内容 |
|---|---|
| 実質的変化の有無 | 効果の有無が逆転する・解釈が変わる → 要注意 |
| オッズ比の変化量(exp) | ±20〜30%以上の差があるとブレが大きいと判断 |
| 統計的有意性の有無 | p値の有意⇔非有意の切り替わりは結論に影響が大きい |
係数をオッズ比に戻すにはexp(estimate)で変換します。
# 各補完パターンで感度分析を実行
results <- map_dfr(names(fill_patterns), function(name) {
filled_df <- df %>%
mutate(diabetes = if_else(is.na(diabetes), fill_patterns[[name]], diabetes))
model <- glm(outcome ~ treatment + diabetes, data = filled_df, family = binomial)
# 結果の整理
tidy(model) %>%
mutate(
pattern = name,
odds_ratio = exp(estimate), # オッズ比の計算
conf.low = exp(estimate - 1.96 * std.error), # 95%信頼区間(下限)
conf.high = exp(estimate + 1.96 * std.error) # 95%信頼区間(上限)
)
})
View(results)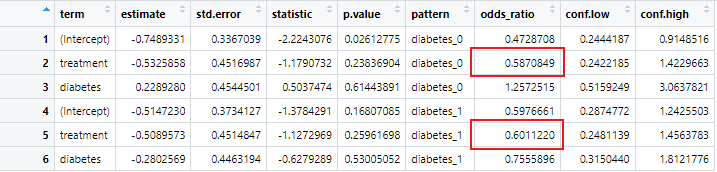

今回は、赤で囲んだ部分を比較したところ、オッズ比の変化も20%以下であり、結果は頑健であると評価できるでしょう。
感度分析で気をつけること
感度分析は「不確かさへの対策」であり、完璧な答えを出すものではありません。また分析結果の解釈は、仮定に依存するため注意が必要です。
そのため、現実的な仮定を選ぶことが重要です。
(例のように極端すぎる補完などは避ける)
まとめ
本記事では、感度分析に関する概略をRの例を交えつつご説明しました!
Rを使えば、簡単なコードで感度分析を行うことができます。
ぜひ、自分の研究やデータ解析に取り入れてみてください!
皆様のお役に立てたなら幸いです。










コメント