こんにちは。ほしのはやしです。
臨床研究を計画する上で欠かせないのが「サンプルサイズ(N数)の設計」です。
サンプルサイズが不適切だと、せっかくの研究も信頼性を欠く結果となりかねません。
この記事では、臨床研究におけるN数の決め方を、概念からRによる具体的な計算方法まで、わかりやすく解説します。
サンプルサイズ設計とは?
臨床研究では「統計的に有意な差が出るか」を調べることが目的です。
しかし、患者数が少なすぎると効果があっても“有意差がない”と判断されるリスクが高まります。逆に多すぎると、リソースの無駄になるだけでなく、倫理的な問題も生じます。
そのため、研究計画の段階でどのぐらいのサンプル数が必要か計算する必要があります。
なぜN数が重要なのか?
サンプルサイズは以下のバランスの上で成り立ちます。
・有意水準(α):通常は0.05(5%)
・検出力(power):通常は80%(0.8)または90%(0.9)
・効果量(effect size):どれくらいの差を検出したいか
・分散(標準偏差):ばらつきが大きいと多くのN数が必要になる
実際には、有意水準・検出力は0.05, 80%で固定になることが多く、効果量を決定することでサンプルサイズを決定することができます!
効果量(Cohen’s d)とは?
効果量(Effect size)とは?
効果量とは、「どれくらいの差が意味のある差なのか」を数値化したものです。
臨床研究においては、単に「差があるか」ではなく、「どれくらい大きな差があるのか」を表すために使います。
Cohen’s d とは?
Cohen’s dは、2群の平均の差を標準偏差で割った値で、2群の差の大きさを「標準化」して比較可能にした効果量です。
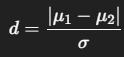
- μ1, μ2:2群の平均値
- σ:標準偏差(2群の共通の標準偏差を使うのが一般的)
Cohen’s d の目安(Cohenの基準)
| 効果量 d | 解釈 |
|---|---|
| 0.2 | 小さい効果(small) |
| 0.5 | 中程度の効果(medium) |
| 0.8 | 大きな効果(large) |
たとえば、薬の効果がCohen’s d = 0.5であれば、「薬とプラセボの差は中程度の大きさがある」と考えられます。
効果量はどうやって決める?
1. 過去の文献・研究を参考にする
同様の対象・アウトカムを扱った論文の報告された差(平均値・SD)を調べて計算
例:
新薬Aの効果:平均10.0
プラセボ群の効果:平均8.0
全体の標準偏差:4.0
→ 効果量 = (10 – 8) / 4 = 0.5(中等度)
2. 臨床的に意味のある差(MCID)をもとに推定する
「これくらいの差が出れば臨床的に意味がある」と考えられる値を専門的判断やガイドラインから設定
例:血圧の差:高血圧治療薬の研究
- 平均血圧の差が 2 mmHg → 統計的には有意かもしれないが、臨床的な意味は薄い。
- 一方、10 mmHg以上 の収縮期血圧低下 → 脳卒中や心血管イベントリスクを明らかに減らすことが知られており、臨床的に有意。
「10 mmHg 以上」がMCIDとされる。
同様の研究の既報から、プラセボ(またはコントロール群)の血圧の標準偏差(例えば、15mmHgとする)を得ることで、以下のように効果量を計算できます。
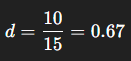
3. 仮定値(シナリオ分析)として仮に設定する
検出したい効果量を複数設定して感度分析(例:d = 0.3, 0.5, 0.8 など)
 星柴くん
星柴くんいろんな方法があるんだね!



効果量さえ決めてしまえば、あとは計算するだけやでな!
サンプルサイズ計算に必要な要素
臨床研究では、対象のタイプによって使う統計手法が変わり、それに応じてN数計算も変わります。
| 比較内容 | 手法 | 使用関数例(R) |
|---|---|---|
| 2群の平均値の差 | t検定 | power.t.test() |
| 2群の割合の差 | カイ二乗・Fisher検定 | power.prop.test() |
| 生存時間解析 | log-rank test | powerSurvEpi::ssizeCT.default() |
| 回帰分析 | 線形・ロジスティック回帰 | pwr.f2.test() など |
実際のRコードで計算してみよう
例1:90日後の新薬とプラセボの血圧の差を評価する試験
効果量:0.5(Cohen’s d)
有意水準:0.05
検出力:0.8
# pwrパッケージのインストール(初回のみ)
install.packages("pwr")
# パッケージpwrの展開
library(pwr)
# 効果量 d = 0.5(中程度の差)の場合
pwr_result <- pwr.t.test(d = 0.5, power = 0.8, sig.level = 0.05, type = "two.sample", alternative = "two.sided")
# 結果を表示
print(pwr_result)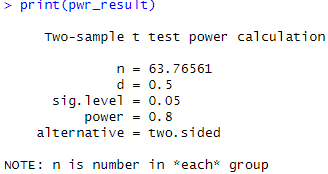

これで、片群あたり約64人必要であることがわかります。
例2:高血圧治療薬の新薬が「生存期間」に影響を与えるか?
ある新しい降圧薬が、心血管イベントを減らし、最終的に 死亡率を下げる(生存期間が延びる) 可能性があると仮定します。
この効果を検証するために、新薬群と従来薬群で生存時間の差があるかを log-rank検定で評価したいとします。
【必要な前提】
| 項目 | 値 |
|---|---|
| 群の割り方 | 1:1(新薬群 vs 従来薬群) |
| 新薬のイベント発生率(死亡率) | 0.2(20%が死亡) |
| 従来薬のイベント発生率(死亡率) | 0.3(30%が死亡) |
| 有意水準(α) | 0.05(両側) |
| パワー(検出力) | 0.8(80%) |
install.packages("powerSurvEpi") # 一度だけ必要
library(powerSurvEpi)
# 新薬群(治療群)のイベント発生率を指定(例:死亡率20% = 0.2)
pE <- 0.2
# 対照群(プラセボ群など)のイベント発生率を指定(例:死亡率30% = 0.3)
pC <- 0.3
# リスク比(RR)を計算:RR = 新薬群の発生率 ÷ 対照群の発生率
# この値が1より小さい場合、新薬の方がイベント発生率が低い(=効果がある)と仮定される
RR <- pE / pC # ここでは 0.2 / 0.3 = 0.6667(=新薬でリスクが約33%減)
# サンプルサイズの計算
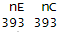
ssizeCT.default(
power = 0.8, # 検出力(Power)=80%。有意差を見逃す確率を20%に設定
k = 1, # 群間の割り付け比。ここでは新薬群と対照群が1:1(等しい人数)
pE = pE, # 新薬群のイベント発生率(上で定義した値)
pC = pC, # 対照群のイベント発生率(上で定義した値)
RR = RR, # 効果の大きさとしてのリスク比(上記で計算して自動入力)
alpha = 0.05 # 有意水準=5%。
)

まとめ
臨床研究におけるサンプルサイズの計算についての基本的な知識について解説しました!
効果量の算出方法、状況別でのサンプルサイズの計算は、特にプロトコール作成時や倫理審査申請時にも重要です。
皆様のお役に立てたなら幸いです。










コメント