こんにちは、ほしのはやしです。
2種類の薬剤を同時に使うと、効果は足し算になるのか?
それとも、お互いを打ち消したり、予想以上に増幅したりするのか?
細胞実験でも臨床でも、薬の併用による効果の変化はとてもよく検討されるテーマです。
このページでは、薬剤 A と B を組み合わせた時に起こり得る効果の種類(相加・拮抗・相乗)と、
それらを統計的に見分けるための考え方について、初心者向けに解説します。
2種類の薬剤 A と B を一緒に使ったときのパターン
まず最初に用語の説明です!
薬剤を2種類使用した場合には、以下の3パターンに分類されます。
① Antagonistic(拮抗)
A と B が同じ経路を奪い合うように働き、1+1 が 1.5 や 1.2 程度しか出ない。
② Additive(相加)
A と B が独立した経路で働き、単純に 1+1 が 2 になる。
③ Synergistic(相乗)
A が B の効きを増幅するなど、何らかの協調作用があり、1+1 が 2より大きくなる。
この 3 つのどれに当てはまるのかを定量的に判定するのが synergy analysis です。
具体的にどのようにやっていくか、解説していきます!
 星柴くん
星柴くんどの分類に当てはまるかを調べることが機序の解明につながったりするのだ!
それぞれの薬剤の特性を調べる
具体的な実験として、薬剤による細胞の生存率を調べる研究を想定します。
今回は、薬剤A、薬剤BでCell viability assayをするイメージとなります。
単剤のDose-response curveを得る
まずは、薬剤A、薬剤BのそれぞれでDose-response curveを作成します。
細胞の生存率を調べる場合には以下の濃度設定をすることが多いです。
0, 10nM, 30nM, 100nM, 300nM, 1μM, 3μM, 10μM, 30μM, 100μM
この10条件で96wellプレートで横10列、縦6行レプリケート(N=6, 複製)で行うのが一つのテンプレートです。
もし薬剤2種類を同一プレートで行いたい場合は、それぞれ縦4行レプリケート(N=4)でやることもできます!
まずは、練習用のデータをRで作成します。
set.seed(123)
# 濃度系列 (μM単位に統一)
dose <- c(0, 0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100)
# Hill関数
hill <- function(dose, EC50, Hill = 1.2) {
100 / (1 + (dose / EC50)^Hill)
}
# 理論曲線
true_A <- hill(dose, EC50 = 0.1) # AのEC50 = 100 nM = 0.1 μM
true_B <- hill(dose, EC50 = 3) # BのEC50 = 3 μM
# ノイズを加えてN=4のデータ生成(下限0に補正)
make_replicate <- function(true_values) {
mat <- replicate(4, true_values + rnorm(length(true_values), 0, 5))
mat[mat < 0] <- 0 # 下限を0に
return(mat)
}
A_mat <- make_replicate(true_A)
B_mat <- make_replicate(true_B)
# EXP列を追加
EXP <- paste0("EXP", 1:4)
# データ整形
library(dplyr)
df_A <- data.frame(
Drug = "A",
Dose_uM = rep(dose, times = 4), # 各EXPが全濃度を測定
EXP = rep(EXP, each = length(dose)), # EXP1~4をそれぞれ10濃度ずつ
Viability = as.vector(A_mat)
)
df_B <- data.frame(
Drug = "B",
Dose_uM = rep(dose, times = 4),
EXP = rep(EXP, each = length(dose)),
Viability = as.vector(B_mat)
)
df <- bind_rows(df_A, df_B)
View(df)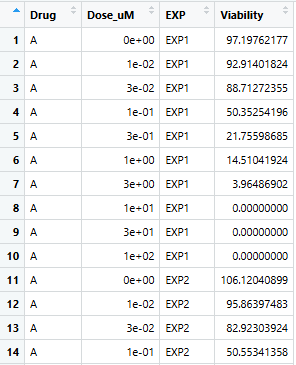

実際の実験結果もこのようなLong形式で、薬剤の種類(Drug)、薬剤濃度(Dose_uM)、実験ナンバー(EXP)、解析結果(Viability)で入力しておきましょう!
今回は、上記のデータをテーブル「df」として作成しています。
ggplotでグラフ化します。
library(tidyverse)
# 平均とSDの計算
df_summary <- df %>%
group_by(Drug, Dose_uM) %>%
summarise(
mean_viability = mean(Viability),
sd_viability = sd(Viability),
.groups = "drop"
)
ggplot() +
geom_point(
data = df,
aes(x = Dose_uM, y = Viability, color = Drug, shape = EXP),
alpha = 0.8,
size = 3
) +
geom_errorbar(
data = df_summary,
aes(x = Dose_uM,
ymin = mean_viability - sd_viability,
ymax = mean_viability + sd_viability,
color = Drug),
width = 0.1,
alpha = 0.7,
linewidth = 1.2
) +
geom_line(
data = df_summary,
aes(x = Dose_uM, y = mean_viability, color = Drug),
size = 1.5
) +
scale_x_log10(
breaks = c(0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100),
labels = c("0.01", "0.03", "0.1", "0.3", "1", "3", "10", "30", "100")
) +
scale_color_manual(values = c("A" = "red", "B" = "blue")) + # 実際のDrug名に合わせる
coord_cartesian(ylim = c(0, 120)) +
labs(
title = "Dose–Response Curves for Drug A and B",
x = "Concentration (μM)",
y = "Cell viability (% of Control)",
color = "Drug"
) +
theme_classic(base_size = 14) +
theme(
legend.position = "right",
panel.grid.minor = element_blank()
) +
guides(shape = "none")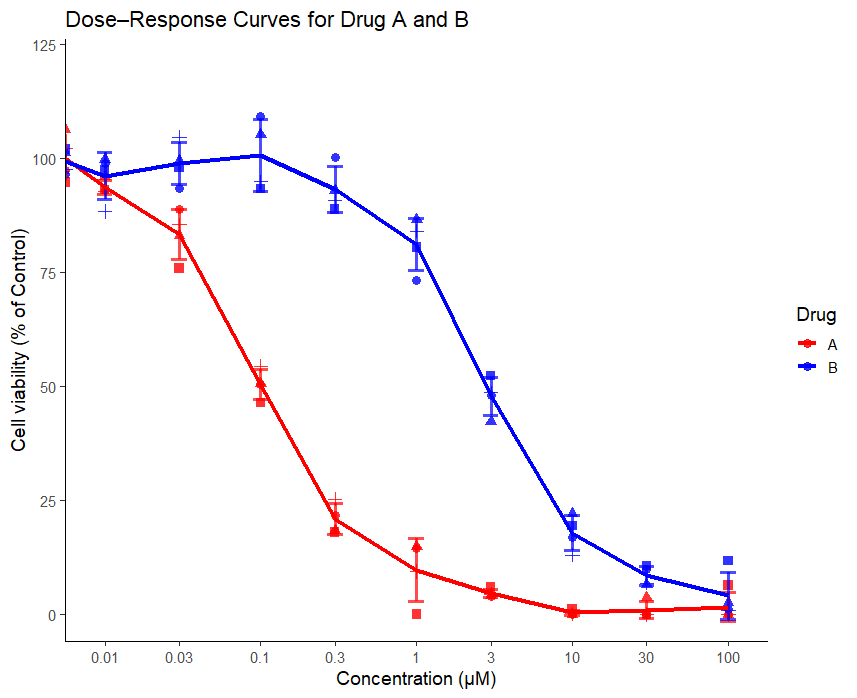




よくみる曲線が得られたのだ!



これでイメージできたと思うから、次に相乗効果の有無を調べていくやで!
Chou-Talalay法に基づくシナジー解析(Synergy analysis)
Chou-Talalay法(Combination Index (CI)法)は、薬物の組み合わせ効果(相乗作用、相加作用、拮抗作用)を定量的に評価するための標準的な方法です。
Dose-response curve(用量反応曲線)が得られている薬剤AとBについて、効率よくシナジー解析を行うための実験について説明します。
1:組み合わせ比率の決定
先程得られた薬剤AとBのIC50から、比率(IC50[A]:IC50[B])を固定比率として決定します。
これを基準にすることで、最も相乗効果が期待できる組み合わせを効率的に調べることができます。
2:幅広い効果レベルをターゲットとした用量設定
この固定比率を維持したまま、組み合わせた”合計用量”が幅広い効果レベルを達成するように実験群を決定します。
- コントロール群:Vehicleコントロール
- 低効果群:25%の細胞死が得られると予測される合計容量
- 中効果群:50%の細胞死が得られると予測される合計容量
- 高効果群:75%の細胞死が得られると予測される合計容量



低効果群とかの合計容量ってどうやって決めるんだろう?



そこも計算して決定できるから、次の章を読むやで!
必要に応じて、10%, 25%, 50%, 75%, 90%, 95% の効果目標値と細分化して精密な結果を得ることもできます。
計算によって得られた合計容量でCell viabilityを見ることで、相乗効果があるかどうか判定することができます。
例えば、低効果群の用量では25%の細胞死が予想されますが、実験結果から35%の細胞死が確認された場合、相乗効果があると判定できます!
具体的なデータ解析の一例
先程のデータセットを用いて、解析に必要なデータを取得していきます。
drc, tidyverseパッケージを使用しますので、未インストールの場合はインストールをしてください。
パッケージのインストール方法はこちら!


1:Hill係数とIC50の計算
library(drc)
library(tidyverse)
# 薬剤Aのデータのみを抽出
df_A <- df %>% filter(Drug == "A")
# log(0)は扱えないため、Doseが0の行は除外します
df_A_log <- df_A %>% filter(Dose_uM > 0)
# モデルの実行
model_A <- drm(Viability ~ Dose_uM, data = df_A_log, fct = LL.4(names = c("Slope", "Lower_Limit", "Upper_Limit", "IC50")))
# モデルの要約を表示
summary(model_A)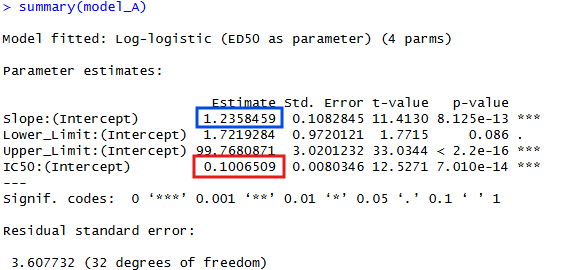

IC50が0.100μM, Hill係数が1.2(青で囲まれた数値の絶対値)であることがわかりました!
同様に薬剤Bも計算します。
# 薬剤Bのデータのみを抽出
df_B <- df %>% filter(Drug == "B")
# log(0)は扱えないため、Doseが0の行は除外します
df_B_log <- df_B %>% filter(Dose_uM > 0)
# モデルの実行
model_B <- drm(Viability ~ Dose_uM, data = df_B_log, fct = LL.4(names = c("Slope", "Lower_Limit", "Upper_Limit", "IC50")))
# モデルの要約を表示
summary(model_B)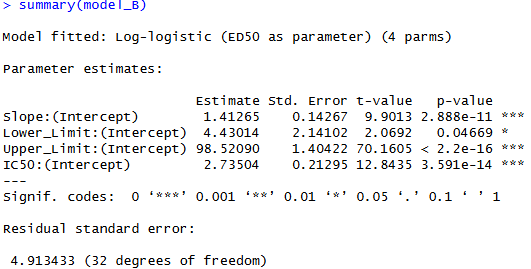

IC50が2.74μM, Hill係数が1.4ですね!
2:組み合わせ比率(固定比率)の計算
続いて固定比率の計算を行います。
# 薬剤AのHill係数を絶対値にしている
coef_A <- coef(model_A)
IC50_A <- coef_A["IC50:(Intercept)"] # 薬剤AのIC50
m_A <- abs(coef_A["Slope:(Intercept)"]) # 薬剤AのHill係数
# 薬剤BのHill係数を絶対値にしている
coef_B <- coef(model_B)
IC50_B <- coef_B["IC50:(Intercept)"] # 薬剤BのIC50
m_B <- abs(coef_B["Slope:(Intercept)"]) # 薬剤BのHill係数
# 固定比率(r)の計算
r <- IC50_A / IC50_B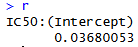

3:予測用量を計算する関数の作成と結果
目的とする効果量が実験によって、25%, 50%, 75%だけなのか、もっと必要なのかによって大きく計算量が変わるので、関数を作成して柔軟に結果が得られるようにします。
# 予測用量計算関数
calculate_predicted_doses <- function(fa_target, IC50_A, m_A, IC50_B, m_B, r) {
# fa_target は 0 から 1 の間の値 (例: 0.25, 0.50)
# 単剤用量 Dx の計算 (ICxに相当)
Dx_A <- IC50_A * (fa_target / (1 - fa_target))^(1 / m_A)
Dx_B <- IC50_B * (fa_target / (1 - fa_target))^(1 / m_B)
# 相加作用の組み合わせ予測用量 (CI=1) の計算
DB_pred <- 1 / ( (r / Dx_A) + (1 / Dx_B) )
DA_pred <- r * DB_pred
# 結果をデータフレームとして返す
return(data.frame(
fa_target = fa_target * 100, # パーセント表示
DA_pred_μM = DA_pred,
DB_pred_μM = DB_pred,
Total_Dose_μM = DA_pred + DB_pred
))
}続いて、この関数「calculate_predicted_doses」を用いて目的の効果レベルに必要な薬剤Aと薬剤Bの終濃度を計算します。
今回は、25%, 50%, 75%の場合で行います。
# 検討したい効果レベル (パーセント) を定義
fa_percentages <- c(25, 50, 75)
# パーセントをfa (0-1) に変換
fa_targets <- fa_percentages / 100
# lapplyを使って全ての目標効果レベルに対して関数を実行し、結果を結合
results_list <- lapply(fa_targets, function(fa) {
calculate_predicted_doses(fa, IC50_A, m_A, IC50_B, m_B, r)
})
# 結果を一つのデータフレームに結合
predicted_doses_df <- do.call(rbind, results_list)
print(predicted_doses_df)

| 列名 | 意味 |
| fa_target | 目標とする細胞死(阻害)の効果レベル。 |
| DA_pred_μM | その効果レベルを相加作用で達成するために必要な薬剤Aの終濃度。 |
| DB_pred_μM | その効果レベルを相加作用で達成するために必要な薬剤Bの終濃度。 |
| Total_Dose_μM | 組み合わせの合計用量。 |
4.実験結果からCombination index(CI)を計算し解釈する
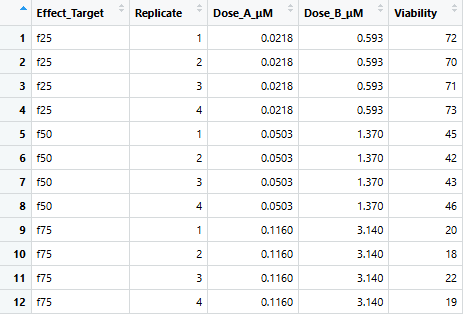
先程の計算結果に基づいて、効果量25%, 50%, 75%になる濃度でCell viability assay (N=4)をしたとします。
説明用に以下の結果が得られたとしましょう。
# 説明用の結果テーブルの作成(本番はエクセルから読み込むことが多い)
dose_25_A <- 0.0218; dose_25_B <- 0.593 # CI=1 と予測された 25%効果の用量
dose_50_A <- 0.0503; dose_50_B <- 1.37 # CI=1 と予測された 50%効果の用量 (計算例より)
dose_75_A <- 0.116; dose_75_B <- 3.14 # CI=1 と予測された 75%効果の用量 (計算例より)
df_result <- data.frame(
Effect_Target = rep(c("f25", "f50", "f75"), each = 4),
Replicate = rep(1:4, 3),
Dose_A_μM = c(rep(dose_25_A, 4), rep(dose_50_A, 4), rep(dose_75_A, 4)),
Dose_B_μM = c(rep(dose_25_B, 4), rep(dose_50_B, 4), rep(dose_75_B, 4)),
# Viability (0-100%) は実験で得られた実測値
Viability = c(
# f25を予測用量で処理した場合 (ここではシナジーを仮定し、Viability < 75%)
72, 70, 71, 73,
# f50を予測用量で処理した場合 (Viability < 50%)
45, 42, 43, 46,
# f75を予測用量で処理した場合 (Viability < 25%)
20, 18, 22, 19
)
)

この結果がdf_resultに格納されているとします。
続いて、実測効果の割合をViabilityから計算します。
# 実測効果の割合 fa_obs (0-1) を計算
df_result <- df_result %>%
mutate(fa_obs = 1 - (Viability / 100))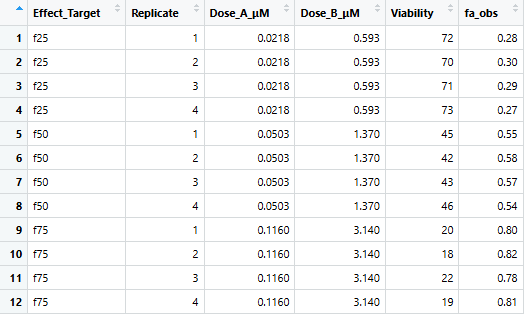

続いて、Combination index (CI)を計算する関数を作成します。
calculate_ci <- function(DA, DB, fa_obs, IC50_A, m_A, IC50_B, m_B) {
if (fa_obs >= 1) {
return(NA) # 効果が100%の場合はCIの定義上、計算不可
}
Dx_A <- IC50_A * (fa_obs / (1 - fa_obs))^(1 / m_A)
Dx_B <- IC50_B * (fa_obs / (1 - fa_obs))^(1 / m_B)
# CI の計算 (Chou-Talalayの式)
CI <- (DA / Dx_A) + (DB / Dx_B)
return(CI)
}この関数を用いて、先程のdf_resultの結果からCIを計算します。
df_ci <- df_result %>%
rowwise() %>% # 行ごとに処理
mutate(
CI = calculate_ci(
DA = Dose_A_μM,
DB = Dose_B_μM,
fa_obs = fa_obs,
IC50_A = IC50_A,
m_A = m_A,
IC50_B = IC50_B,
m_B = m_B
)
) %>%
ungroup()
# 目標効果レベルごとの集計
ci_summary <- df_ci %>%
group_by(Effect_Target) %>%
summarise(
N_Replicates = n(),
Mean_CI = mean(CI, na.rm = TRUE),
SD_CI = sd(CI, na.rm = TRUE),
SE_CI = SD_CI / sqrt(N_Replicates),
CI_Lower = Mean_CI - qt(0.975, df = N_Replicates - 1) * SE_CI,
CI_Upper = Mean_CI + qt(0.975, df = N_Replicates - 1) * SE_CI
)
print(ci_summary)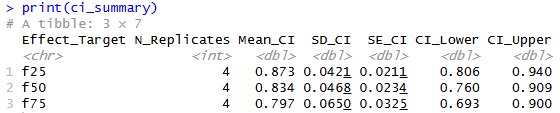

これで各効果量におけるCIが計算できました!
結果の解釈は以下が一つの方法です。
| 95% 信頼区間 | 統計的結論 | 相互作用 |
| CI_Upper < 1.0 | 有意差あり | 相乗作用 (Synergy) |
| CI_Lower >1.0 | 有意差あり | 拮抗作用 (Antagonism) |
| 1.0を跨ぐ | 有意差なし | 相加作用 (Additive) |
今回の結果では、25%, 50%, 75%のすべての効果量でCI_Upperが1.0未満であり、有意差を以て相乗作用がありと判定できました!



相乗効果のあるかないかについて判定する方法を学んだのだ!



計算がいっぱいで大変やけど、やればFigureになるから頑張るんやで!
まとめ
相乗効果を判定するための具体的な方法について解説しました!
複数の薬剤を組み合わせた研究は、臨床的意義だけでなく新たな機序解明につながることもあるので、とても重要ですね!
このページが少しでもお役に立てたなら幸いです!










コメント