こんにちは。ほしのはやしです。
統計って聞くだけでアレルギーが出て、本や画面をそっ閉じ…ありますよね。
細かいことが気になり始めると手につかなかったりするので、まずはパターン事に理解するのが大事です。
このページでは、対応のあるなし、正規分布かどうかに基づいて2つの数値を比較する場合の統計手法を一気に解説します!
R studioでの使用を想定して、簡単なスクリプトも紹介します。
R studioのインストール方法は下記を参考にしてください!

対応のあるデータとは?
対応のあるデータとは、同じ対象について異なる条件下で測定されたデータのことです。
文字通り、データ同士にペアの関係がある(対応している)ということです。
例1:ダイエットの効果測定
- 対象: ある会社の社員
- 測定項目: 体重
- 異なる条件: ダイエット前、ダイエット後
この場合、ダイエット前後の体重を比較することで、ダイエットの効果を評価することができます。
ダイエット前とダイエット後は、同じ人が測定対象なので、対応のあるデータとなります。
例2:新薬の効果測定
- 対象: 心筋梗塞の患者
- 測定項目: 血圧
- 異なる条件: 新薬服用前、新薬服用後
新薬服用前後の血圧を比較することで、新薬の効果を評価することができます。
この場合も、同じ患者が測定対象なので、対応のあるデータとなります。
例3:学習方法の効果測定
- 対象: ある特定の学生
- 測定項目: テストの点数
- 異なる条件: 従来の学習法、新しい学習法
同じ学生が異なる学習法でテストを受けた場合、それぞれのテストの点数を比較することで、学習方法の効果を評価することができます。
このようなケース以外の場合を「対応がない」として、2つの数値を比較することになります!
正規分布、非正規分布とは?
正規分布は、自然界や社会現象において最もよく見られる確率分布の一つです。
「釣鐘型分布」とも呼ばれ、データの多くが平均値の近くに集まり、両側に裾野が広がるような形をしています。
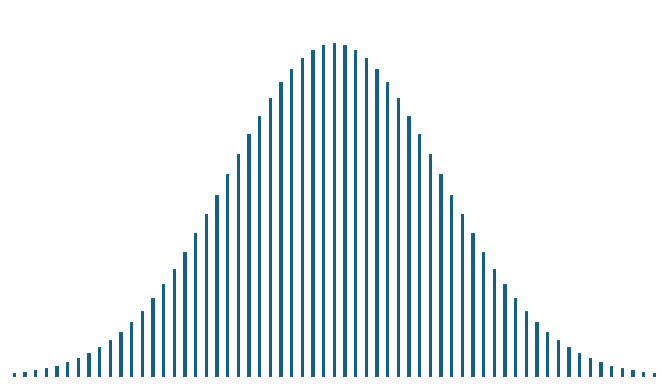
一方で、正規分布以外の確率分布を総称して、非正規分布といいます。
正規分布と異なり、データの分布が左右対称でない、裾野が極端に長いなど、様々なパターンがあります。
非正規分布の場合は、以下の図のようにどちらかに偏っていたり、バラバラの分布だったりします。
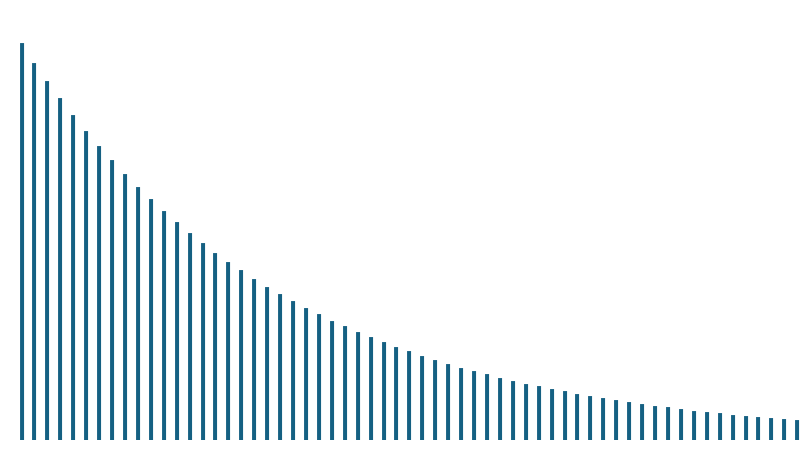
 星柴くん
星柴くん対応のある・なし、正規分布についてイメージがついたのだ!



まずはここを抑えないとどの統計使ったらよいかわからんでな
2つ数値を比較(対応のないt検定:正規分布:パラメトリック)
まずはオーソドックスな、対応のない・正規分布のケースについてご説明します!
3年B組(それぞれ15人ずつ)の男子と女子の身長が統計的に差があるか調べたい!
こんなときに使うパターンです。
他には、血圧の薬を飲んでる人と飲んでない人で血圧に差があるか、などに使えます。
R studioのコードの例
【男子と女子の身長の統計差を調べたい】
テーブル名:datasheet1
| Hight | Sex |
|---|---|
| 155 | Male |
| 160 | Male |
| 140 | Female |
| 145 | Female |
| 158 | Male |
| … | … |
t.test(Hight~Sex, data = datasheet1, var.equal = FALSE)
【構文の形】
t.test(数値の列名~グループの列名, data = 読み込んだテーブルの名前, var.equal = FALSE)
という構文が基本になります。
ここでは「Hight」=「身長」, 「Sex」=「性別」としています。
2つの数値を比較(対応のあるt検定:正規分布:パラメトリック)
3年B組30人のテストの点の平均点が、キンパツ先生が来る前と後で違うか調べたい!
こんなときに使います。
同じ人や物で、数値が変化した前後を調べたいときに使う統計手法です。
R studioのコードの例
【コードの例:キンパツ先生の来る前後でクラスのテストの点の統計差を調べたい】
テーブル名:datasheet2
| Test1 | Test2 |
|---|---|
| 70 | 80 |
| 65 | 70 |
| 80 | 75 |
| 50 | 90 |
| 75 | 70 |
| … | … |
t.test(Test1, Test2, data = datasheet2, paired = TRUE)
【構文の形】
t.test(数値の列名1, 数値の列名2, data = 読み込んだテーブルの名前, paired = TRUE)
このpaired = TRUEで対応のあることを示しているわけですね!
もし表のパターンが以下のようなときは、別のコードで統計することができます!
テーブル名:datasheet3
| No | Score | Kinpatsu |
|---|---|---|
| 1 | 70 | before |
| 1 | 80 | after |
| 2 | 65 | before |
| 2 | 70 | after |
| 3 | 80 | before |
| 3 | 75 | after |
| … | … | … |
t.test(Score~Kinpatsu, data = datasheet3, paired = TRUE)
【構文の形】
t.test(数値の列名1~タイミングの列名2, data = 読み込んだテーブルの名前, paired = TRUE)
通常はdatasheet2のようなパターンでエクセルファイルを作るのをオススメします。
さて、ここまで正規分布するパターンを前提に解説しました。
これらの統計手法をパラメトリック法といいます。
正規分布しない場合についての統計手法(ノンパラメトリック法)、次の項目で引き続き解説します。
2つの数値を比較(対応のない:非正規分布:ノンパラメトリック検定:Wilcoxonの順位和検定)
正規分布しない(またはわからない)場合は、Wilcoxonの順位和検定を使用するのが最も簡単です。
先程の「datasheet1」の場合を想定してコードを示します。
テーブル名:datasheet1
| Hight | Sex |
|---|---|
| 155 | Male |
| 160 | Male |
| 140 | Female |
| 145 | Female |
| 158 | Male |
| … | … |
wilcox.test(Hight~Sex, data = datasheet1)
【構文の形】
wilcox.test(数値の列名~グループの列名, data = 読み込んだテーブルの名前)
2つの数値を比較(対応のある:非正規分布:ノンパラメトリック検定:Wilcoxonの符号付き順位検定)
正規分布しないバージョンの「対応のあるt検定」が、Wilcoxonの符号付き順位検定です。
先程の「datasheet2」の場合を想定してコードを示します。
テーブル名:datasheet2
| Test1 | Test2 |
|---|---|
| 70 | 80 |
| 65 | 70 |
| 80 | 75 |
| 50 | 90 |
| 75 | 70 |
| … | … |
wilcox.test(Test1, Test2, data = datasheet2, paired = TRUE)
t.test(Test1, Test2, data = datasheet2, paired = TRUE)
これで数値比較の基本パターンは終了です!
棒グラフとドットプロットを重ねてグラフを描く方法
練習用のデータをR studioを使って作成
group <- c(rep(“A”, 10), rep(“B”, 10))
value <- c(rnorm(10, mean = 10, sd = 2), rnorm(10, mean = 12, sd = 3))
data <- data.frame(group, value)
groupという列にAが10個、Bが10個。
valueという列にランダムに平均10, 標準偏差2となるように10個数値を作成し、続いて平均12, 標準偏差3となるように10個数値を作成しています。
データシート名:data
| group | value |
|---|---|
| A | 9.790517 |
| A | 5.379381 |
| A | 9.374840 |
| … | … |
| B | 7.708036 |
| B | 12.356714 |
平均値と標準偏差を計算
library(tidyverse)
data_summary <- data %>%
group_by(group) %>%
summarise(
mean_value = mean(value),
sd_value = sd(value)
)
data_summaryという新しいテーブルに、グループ毎での平均値と標準偏差を出しています。
グラフの作成
ggplot(data_summary, aes(x = group, y = mean_value)) +
geom_bar(stat = “identity”, fill = “gray”, colour = “black”) + # 棒グラフ
geom_errorbar(aes(ymin = mean_value – sd_value, ymax = mean_value + sd_value), width = 0.3) + # 誤差棒
geom_point(data = data, aes(x = group, y = value), size = 4, colour = “black”, fill = “black”, position = position_jitter(width = 0.2)) + # 黒いドット
geom_hline(yintercept = 0, color = “black”, size = 1) + # 0のラインを描画
labs(x = “グループ”, y = “値”, title = “2群の比較”) +
theme(
axis.line.x = element_blank(), # X軸の線を消す
axis.line.y = element_line(color = “black”, linewidth = 1), # Y軸の線を維持
axis.text = element_text(color = “black”, size = 18, face = “bold”), # 軸ラベルのスタイル
axis.title = element_text(size = 24), # 軸タイトルのスタイル
panel.background = element_blank(), # 背景を透明に
axis.ticks.length = unit(-2, “mm”), # 軸目盛りの長さ
axis.ticks = element_line(color = “black”, size = 1), # 軸目盛り線のスタイル
legend.position = “none” # 凡例を非表示
)
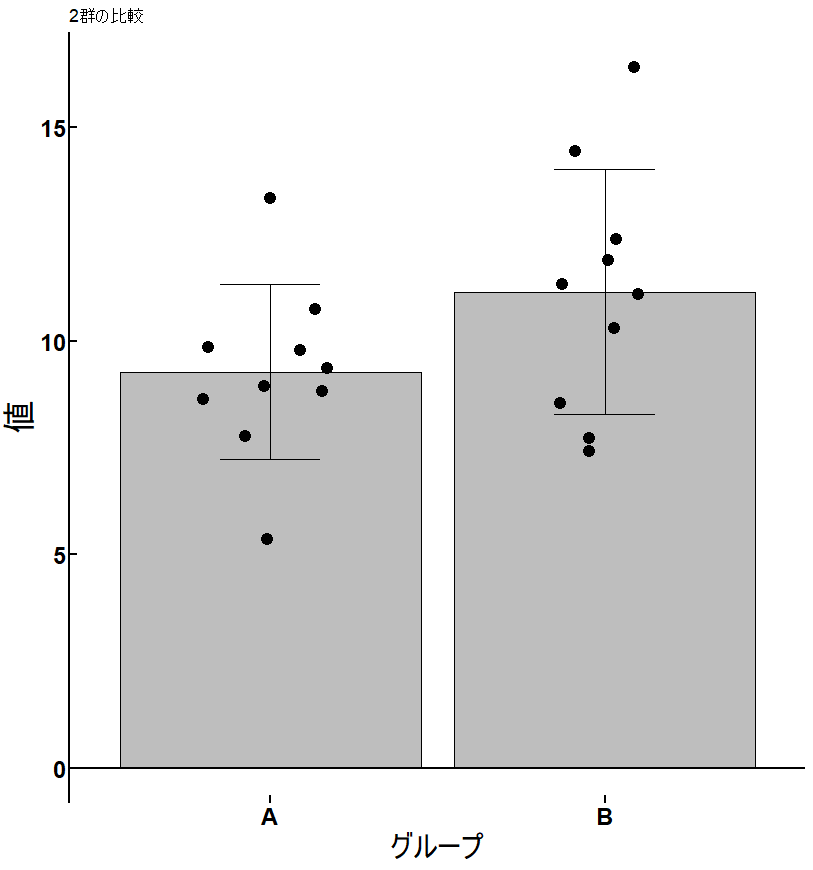

まとめ
2つの数値を統計的に比較する場合の基本4パターンについて解説しました。
少しでも統計について慣れていただけると幸いです!
| 正規分布 | 対応のない | 対応のある |
|---|---|---|
| する | t検定 | 対応のあるt検定 |
| しない(わからない) | Wilcoxonの順位和検定 | Wilcoxonの符号付き順位検定 |










コメント