【初心者向け】競合リスク分析・Gray検定・累積発生率のグラフ化をRでやる方法

2024年12月26日

URLをコピーしました！

こんにちは。ほしのはやしです。

カプランマイヤー曲線を勉強すると、「これって本当に打ち切りでいいの？」とか「競合リスク分析？」とかいろんな疑問点が出てきますよね。

このページでは、これらについての概略と、Rで実際にどのような流れで統計分析してグラフ描画を行うかについて解説していきます！！

競合リスク分析(Competing Risk Analysis)とは？

競合リスク分析は、複数の相互排他的なイベントが発生する可能性がある場合に使われる統計的手法です。

たとえば、臨床研究では、ある治療の効果を検証する際、患者が「特定の病気で死亡する」以外にも「他の原因で死亡する」リスクが存在します。
このような状況では、異なるリスクが競合し、標準的な生存分析（たとえばKaplan-Meier法）が適切でないことがあります。

【例：ガンに対する新規治療を試した臨床試験の場合】
Kaplan-Meier法は、他のリスク（例：副作用による死亡）を「打ち切り」として扱います。
競合リスクでは、「打ち切り」ではなく、別の重要な出来事として扱う必要があります。

他のリスクを単純に「無視」すると(打ち切りにすると)、元々調べたいリスク（ガンによる死亡）の発生確率が、本来よりも高く見積もられる可能性がある。

競合リスク分析では、それぞれのリスク（イベント）を独立したものとして扱わず、競合関係を考慮して解析します。このアプローチで以下を明らかにすることを目的とします。

各競合イベントの累積発生率（Cumulative Incidence Function, CIF）
あるイベントのリスクが他のリスクによってどのように影響を受けるか

これらを考慮したい場合は、Kaplan-Meier法ではなく競合リスク分析を行うことが必要です。
Kaplan-Meier法について解説した記事は以下の記事をご覧ください。

Gray検定とは？

Gray検定（Gray’s Test）は、競合リスクデータにおける累積発生率の差を統計的に検定するための方法です。

これは、2つ以上の群間で特定のイベントのリスクに有意差があるかを調べる際に使われます。

競合リスクがある生存期間分析ならGray検定
競合リスクがない場合の生存期間分析ならLog-rank検定

例：免疫チェックポイント阻害剤（ICI）の効果評価

免疫チェックポイント阻害剤は、メラノーマ患者の治療において生存率を向上させる有望な治療法です。
しかし、患者は次のような競合するリスクを抱えています：

メラノーマの進行による死亡
ICI治療の副作用や他の原因による死亡

標準的な生存分析（Kaplan-Meier法）は、２のリスクを生存曲線において「発生しない」と仮定するため、競合リスクを正確に評価できません。競合リスク分析を用いると、特定のリスク（メラノーマによる死亡）を正確に解析しながら、他のリスク（副作用による死亡）を考慮できます。

これにより、治療の効果やリスクのバランスを正確に評価し、医療の意思決定に役立てることが可能です。

競合リスクがある場合のグラフはなにか？
（累積発生率：Cumulative Incidence Function）

競合リスクの解析では、累積発生率（Cumulative Incidence Function, CIF）を描くことで、特定のリスクの発生状況を視覚的に評価します。
この手法は、Kaplan-Meier法とは異なり、他の競合するリスクを考慮した上でリスクの推移を描くことができます。

累積発生率（CIF）とは？

累積発生率は、時間の経過とともに特定のリスク（イベント）が発生する確率を示します。
競合リスクがある場合、次のような計算が行われます。

特定のリスクに基づく発生確率を評価
他のリスクの影響を考慮

例えば、メラノーマ患者において「メラノーマによる死亡率」と「副作用による死亡率」を個別に累積発生率として描くことで、それぞれのリスクが時間経過に伴ってどのように増加するかを観察できます。

なぜKaplan-Meier法ではダメなのか？

Kaplan-Meier法は、以下の理由で競合リスクを適切に表現できません。

1. 他のリスクを「打ち切り」として扱う

Kaplan-Meier法では、競合する他のリスク（例えば副作用による死亡）を単純に「観察できなかった」とみなします。これにより、調べたいリスク（例えばメラノーマによる死亡）の発生率が過大評価されてしまいます。

2. 全体のリスクを正確に反映しない

Kaplan-Meier曲線は、競合リスクが存在しない状況を前提とするため、現実に即したリスク評価ができません。

3. 累積発生率を分けて解析できない

Kaplan-Meier法は「あるリスクに限定した解析」が困難です。
一方、競合リスク分析では、特定のリスクに限定した累積発生率を算出できます。

R studioを使った実際の解析例

練習用データの作成

「メラノーマ患者において、免疫チェックポイント阻害剤（ICI）を既存治療法と比較して、副作用による競合リスクを加味して生存率を比較したい」

set.seed(123) # 再現性のための乱数シード

# 患者数
n_patients <- 200

# 患者の特性を生成
age <- round(rnorm(n_patients, mean = 65, sd = 10)) # 年齢（平均65歳、標準偏差10歳）
sex <- sample(c(0, 1), n_patients, replace = TRUE)  # 性別（0: 女性, 1: 男性）
stage <- sample(1:4, n_patients, replace = TRUE, prob = c(0.2, 0.3, 0.3, 0.2)) # ステージ（1-4）
ecog_ps <- sample(0:2, n_patients, replace = TRUE, prob = c(0.5, 0.3, 0.2))    # ECOG-PS（0-2）
pdl1 <- round(runif(n_patients, min = 0, max = 100))                           # PD-L1発現率（0-100%）
Treatment <- sample(c(0, 1), n_patients, replace = TRUE) # 0: 既存治療, 1: ICI治療

# 生存時間とイベントタイプを生成
time <- numeric(n_patients)

for (i in 1:n_patients) {
    if (Treatment[i] == 0) {
        # 既存治療群: 生存時間を指数分布で生成（rate=0.1）
        time[i] <- round(rexp(1, rate = 0.1))
    } else {
        # ICI治療群: 生存時間を指数分布で生成（rate=0.05、つまり生存期間が長くなる）
        time[i] <- round(rexp(1, rate = 0.05))
    }
}

# 副作用死亡とガン死亡の確率をTreatment群に基づいて調整
event <- numeric(n_patients)

for (i in 1:n_patients) {
    if (Treatment[i] == 0) {
        # 既存治療群: ガン死亡の確率を0.4、副作用死亡の確率を0.2
        event[i] <- sample(c(0, 1, 2), 1, prob = c(0.4, 0.4, 0.2))
    } else {
        # ICI治療群: ガン死亡の確率を0.1、副作用死亡の確率を0.2
        event[i] <- sample(c(0, 1, 2), 1, prob = c(0.7, 0.1, 0.2))
    }
}

# イベントをファクター型に変換
event <- factor(event, levels = c(0, 1, 2), labels = c("Censored", "Cancer Death", "Drug Death"))

# データフレームにまとめる
MelaICI <- data.frame(
    ID = 1:n_patients,
    Age = age,
    Sex = factor(sex, levels = c(0, 1), labels = c("Female", "Male")),  # 性別を因子に変換
    Stage = factor(stage, levels = 1:4, labels = c("Stage 1", "Stage 2", "Stage 3", "Stage 4")), # ステージを因子に変換
    ECOG_PS = factor(ecog_ps, levels = 0:2, labels = c("ECOG 0", "ECOG 1", "ECOG 2")), # ECOG-PSを因子に変換
    PD_L1 = pdl1,
    Treatment = factor(Treatment, levels = c(0, 1), labels = c("Conventional Treatment", "ICI Treatment")), # 治療群を因子に変換
    Time = time,
    Event = event
)

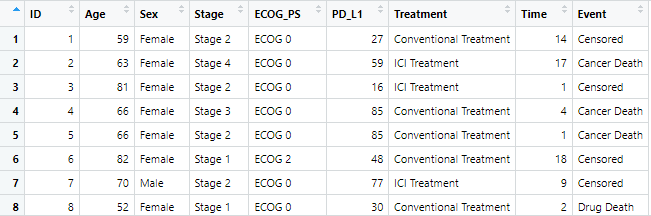
このようにデータシート：MelaICIを作成しました！

Gray検定の方法

続いてGray検定を行います。
パッケージ「tidycmprsk」が必要なので以下のスクリプトでインストールして適応してください。

install.packages("tidycmprsk") # 初回のみ必要
library(tidycmprsk) # 毎回必要

もしインストールできない場合は、Rのバージョンが古い可能性があります。
R studio、Rともに最新のバージョンにアップデートしてください。

実際のGray検定のコードを続いて記載します。

result1 <- cuminc(Surv(Time, Event)~Treatment, MelaICI)
resull1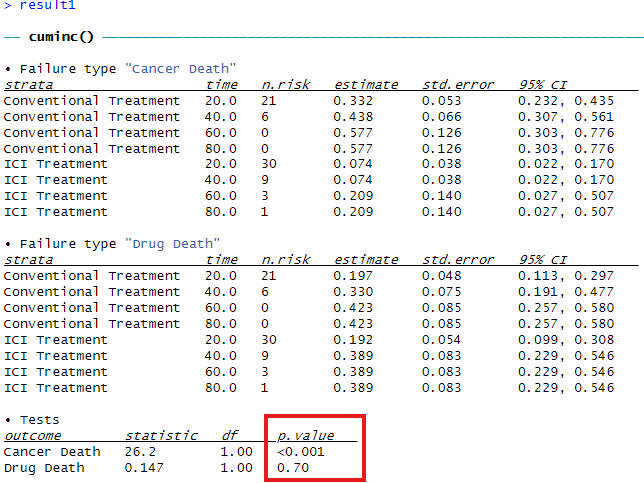

cuminc(Surv(生存期間の列名, イベント発生の種類の列名)~群分けしたい列名, データシート名)

Gray検定の結果の解釈

先ほどの結果の読み方について解説をします。

各列の意味:

Failure type:
競合イベントの種類（Cancer DeathまたはDrug Death）です。
この結果は、ガン死亡と副作用死亡に関する累積発生率が別々に計算されていることを示しています。
strata (治療群):
治療群の名前です。
Conventional Treatment（既存治療）とICI Treatment（免疫チェックポイント治療）の2つの治療群についての分析が行われています。
time (時間):
各時間点での累積発生率の計算が行われています。
例えば、10.0は治療後10ヶ月目、20.0は20ヶ月目のデータです。
n.risk (リスクセットの人数):
各時間点で生存していて、まだイベントが発生していない患者の数です。
この人数は時間とともに減少します。
estimate (累積発生率の推定値):
各時間点での競合イベント（ガン死亡または副作用死亡）の累積発生率（CIF）です。
例えば、一番上の0.332は、10ヶ月目にConventional Treatment群でガン死亡が発生する累積確率が33.2%であることを示します。
std.error (標準誤差):
各推定値に対する標準誤差です。
推定値の信頼性を示す指標で、小さいほど信頼性が高いことを示します。
95% CI (95%信頼区間):
推定値の95%信頼区間です。この区間内に真の累積発生率が含まれると95%の確率で考えられます。
例えば、一番上の0.232, 0.435は、Conventional Treatment群で10ヶ月目におけるガン死亡の累積発生率の95%信頼区間が23.2%から43.5%の範囲にあることを示します。

解析結果の解釈:

1. Cancer Death (ガン死亡)

Conventional Treatment:
- 10ヶ月目のガン死亡累積発生率は0.332（33.2%）。時間が経過するにつれてガン死亡率は増加し、最終的には60ヶ月目で0.577（57.7%）に達します。
ICI Treatment:
- 10ヶ月目のガン死亡累積発生率は0.074（7.4%）と、Conventional Treatment群よりもかなり低いです。時間が経過しても、ICI Treatment群のガン死亡率は低く、60ヶ月目でも0.209（20.9%）であり、Conventional Treatment群よりも低い水準を維持しています。
統計的有意性:
- p値は<0.001であり、Cancer Deathに関して治療群間で有意な差があることを示しています。つまり、Conventional TreatmentとICI Treatmentの間でガン死亡率に有意な差があると結論できます。

2. Drug Death (副作用死亡)

Conventional Treatment:
- 10ヶ月目の副作用死亡累積発生率は0.197（19.7%）。時間が経過するにつれて副作用死亡率は増加し、最終的には60ヶ月目で0.423（42.3%）に達します。
ICI Treatment:
- 10ヶ月目の副作用死亡累積発生率は0.192（19.2%）で、Conventional Treatment群よりも高いです。その後、時間が経過するにつれてICI Treatment群の副作用死亡率も増加しますが、最終的には40ヶ月目で0.389（38.9%）に達します。
統計的有意性:
- p値は0.70であり、副作用死亡に関して治療群間で有意な差がないことを示しています。これは、Conventional TreatmentとICI Treatmentの間で副作用死亡に有意な差がないことを示唆します。

結論:

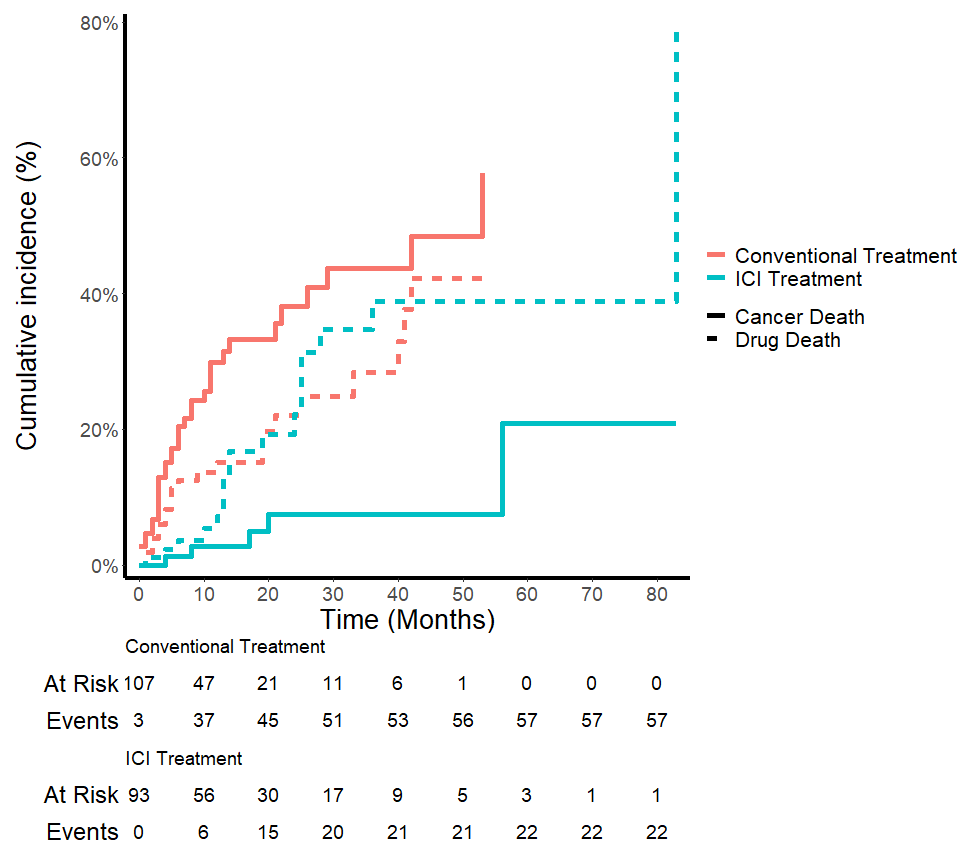
ガン死亡に関して、ICI治療はConventional Treatmentよりも有意に低い累積発生率を示しています。
この結果は、ICI治療がガン死亡リスクを低減する可能性を示唆しています。
副作用死亡に関しては、治療群間に有意な差はない（p値は0.70）。
つまり、副作用による死亡は、ICI治療と従来治療で同程度のリスクで発生していることが分かります。

累積発生率：Cumulative incidence functionのグラフの描き方

install.packages("ggsurvfit") # 初回のみ必要
library(ggsurvfit) # 毎回必要

パッケージ『ggsurvfit』をインストールして展開します。
グラフ自体は先程の【result1】のデータから書きます。

result1 <- cuminc(Surv(Time, Event)~Treatment, MelaICI)

ggcuminc(
    result1,
    outcome = c("Cancer Death","Drug Death"),
    size = 2,
    theme = list(theme_classic())
    )+
    
    # リスクテーブルの表示と各種文字サイズの変更
    add_risktable(
    size = 5,
    theme = theme_risktable_default(axis.text.y.size = 18, plot.title.size = 14)
    ) +
    
    # 必要に応じて線の種類を変更できる
    scale_ggsurvfit()+
    
    # グラフの外観の調整
    theme(
        axis.line = element_line(size = 1.5),  # X軸、Y軸の線の太さ
        axis.title.x = element_text(size = 20),  # X軸のタイトル文字サイズ
        axis.title.y = element_text(size = 20),  # Y軸のタイトル文字サイズ
        axis.text.x = element_text(size = 14),  # X軸の目盛りの文字サイズ
        axis.text.y = element_text(size = 14),   # Y軸の目盛りの文字サイズ
        legend.text = element_text(size = 16)  # 凡例のタイトル文字サイズ
    ) +
    
    # 軸のタイトルの変更
    labs(
        x = "Time (Months)",  # X軸のタイトル名
        y = "Cumulative incidence (%)"   # Y軸のタイトル名
    )