こんにちは。ほしのはやしです。
実験系、コホート系など問わず、外れ値をどう扱うか非常に難しいですよね!
このページでは、「そもそも外れ値とはなにか?」「外れ値が問題になる理由」「実際にRで外れ値を判定する方法」について解説していきます!
外れ値とは?
外れ値とは、データセット内の他の値と比べて著しく異なった値のことです。
この外れ値は様々な原因で発生します。
- 測定誤差:機器の誤動作、人間の操作ミスなど
- サンプルの異質性:実験条件の違い、個体差など
- データ入力ミス
細胞実験など均質な環境の場合は、主に測定誤差・データ入力ミスが原因です。
一方、動物実験・ヒト研究などでは、サンプルの異質性が原因であることが多いです。
外れ値が問題になる理由
外れ値をそのままにしておくことは下記の理由で問題になります。
- 平均値、標準偏差などの統計量を歪ませる
- 回帰分析などのモデルの精度を低下させる
- 誤った結論を導く可能性がある
 星柴くん
星柴くん外れ値があることで、真実が隠れてしまったり、真実ではないことがあたかも真実かのように見えちゃうんだね



だから外れ値をどう扱うべきか学ぶことは非常に重要やでな!
では、どうやって外れ値と認定すべきかどうか。
これを考えることが研究・解析をする上で非常に重要になってきます。
次のセクションでは、外れ値の判定方法や注意点について解説していきます。
外れ値の判定方法
判定手法を用いる前にすること
- データ入力ミスはないか?
- 測定機械に不調はないか?
- サンプルの保存方法に間違いはないか?
- (可能なら)残存している同じサンプルを用いて再現性のある外れ値が検出されるか?
- サンプルや試薬に違和感(細胞なら成長速度、マウスなら体重・毛色、試薬ならロットNoに消費期限)はないか?
まずこれらを確認して、外れ値を疑うデータが「そもそも解析するにふさわしくない(正しくない)」データであるならば、解析からは除外する必要があります。
一方で、実際には再現性をもって外れ値が確認されて、かつ予測されるデータの範囲内でもあり得る、という状況になることも多く、その場合には統計的手法を以て、「外れ値の除外が恣意的でない」ことを主張する必要があります。
具体的な判定方法について解説します。
箱ひげ図を用いた外れ値判定
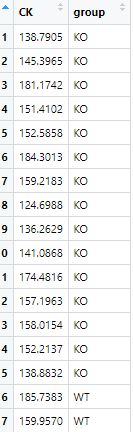
まずは練習用データとして動物実験(WT群とKO群)でCKの値を測定したケースを想定します。
# ライブラリの読み込み
library(tidyverse)
# データ生成
set.seed(123)
CK_normal <- rnorm(27, mean = 150, sd = 20)
CK_outliers <- c(50, 300)
CK <- c(CK_normal, CK_outliers)
# グループ情報を追加
df <- data.frame(CK, group = c(rep("KO", 15), rep("WT", 14)))これでCKという列名のデータシート:dfが作成されました!

以下のコードで箱ひげ図を作成します。
# 必要なパッケージを読み込み
library(ggpubr)
# 外れ値を特定
Q1 <- quantile(df$CK, 0.25) # df$CKはデータシート名$列名で適宜変更
Q3 <- quantile(df$CK, 0.75) # df$CKはデータシート名$列名で適宜変更
IQR <- Q3 - Q1
lower_bound <- Q1 - 1.5 * IQR
upper_bound <- Q3 + 1.5 * IQR
df$outlier <- ifelse(df$CK < lower_bound | df$CK > upper_bound, "Outlier", "Normal") # df$CKはデータシート名$列名で適宜変更。df$outlierのdfもデータシート名に応じて変更
# 外れ値のみのデータフレームを作成。dfはデータシート名に応じて変更
outliers <- df[df$outlier == "Outlier", ]
# 箱ひげ図を作成(df, group, CKはデータシート名, 列名に応じて変更)
ggboxplot(
data = df,
x = "group",
y = "CK",
color = "group", # グループごとに色を分ける
title = "Boxplot of CK by Group with Outlier Labels"
) +
geom_text(
data = outliers,
aes(x = group, y = CK, label = round(CK, 2)), # 外れ値の数値を表示
nudge_x = 0.2, # ラベルを少し右にずらす
color = "red", # ラベルの色
size = 5 # ラベルのフォントサイズ
)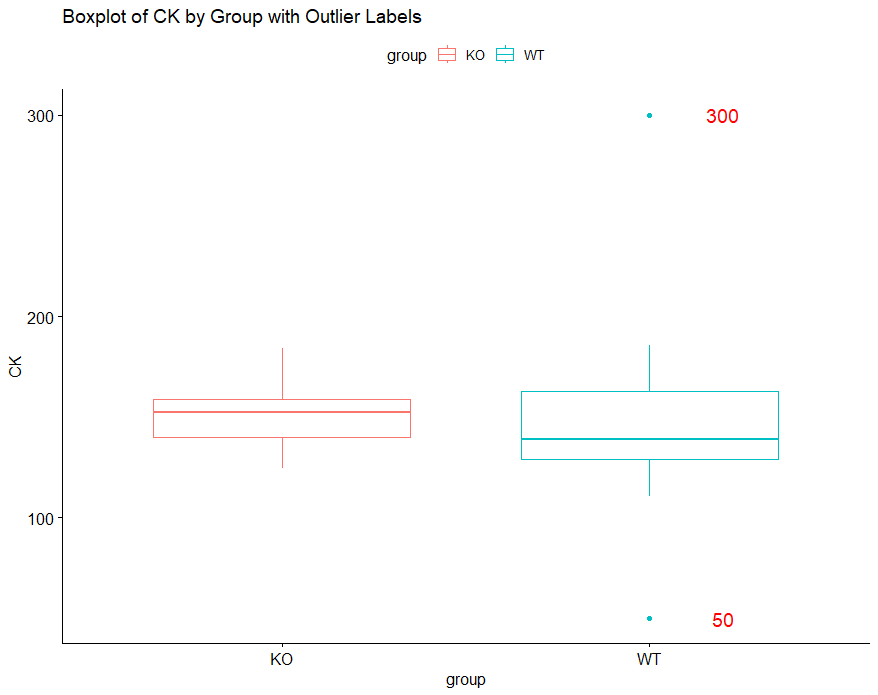

このように外れ値がひと目見てわかるようにできました!
これでこの2つが外れ値と統計的な根拠を得ることができました!
Zスコアを用いた外れ値判定
Zスコアとは?
Zスコアは、データが「平均からどれくらい離れているか」を標準偏差を基準にして数値化した指標です。
標準化されたスケールを使うことで、異なるデータセットや異なる単位のデータでも比較ができるようになります。
Zスコアの計算式:
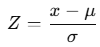
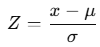
- x : 各データ点
- μ: データ全体の平均
- σ: データ全体の標準偏差
以上の計算式で±2もしくは±3以上離れているデータを外れ値と定義します。
同じデータシートを用いて以下のコードで解析します。(±2以上離れている点を外れ値とする)
# グループごとにZスコアを計算
df <- df %>%
group_by(group) %>%
mutate(
z_score = (CK - mean(CK)) / sd(CK), # グループごとにZスコアを計算
outlier = ifelse(abs(z_score) > 2, "Outlier", "Normal") # Zスコアが±2を超える場合を外れ値と判定
)
# 外れ値のみのデータフレームを作成
outliers <- df %>% filter(outlier == "Outlier")
# 箱ひげ図を作成
ggboxplot(
data = df,
x = "group",
y = "CK",
color = "group", # グループごとに色を分ける
title = "Boxplot with Group-wise Z-Score Outliers"
) +
geom_text(
data = outliers,
aes(x = group, y = CK, label = round(CK, 2)), # 外れ値の数値を表示
nudge_x = 0.2, # ラベルを少し右にずらす
color = "blue", # ラベルの色
size = 5 # ラベルのフォントサイズ
)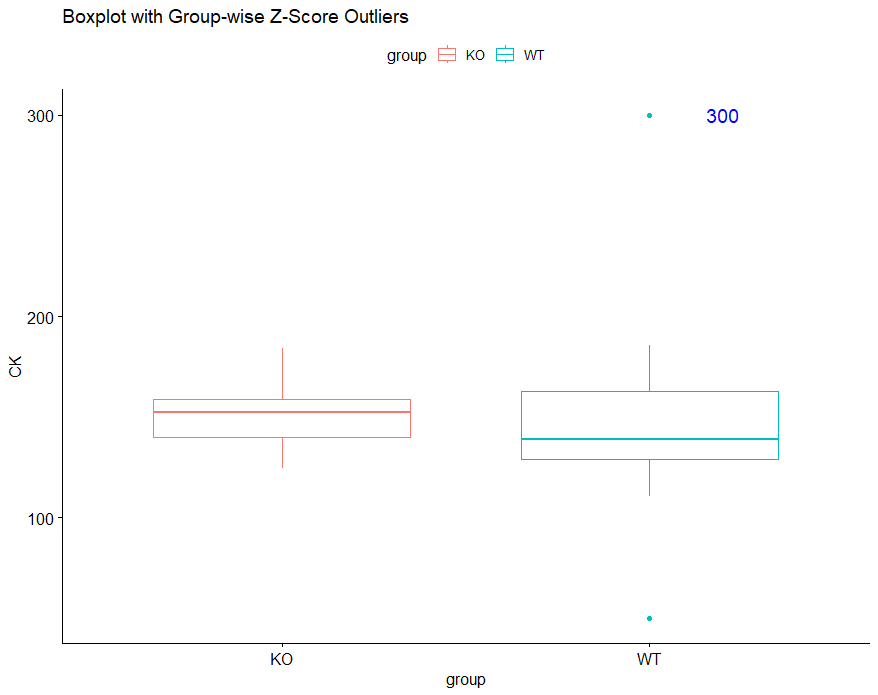

このように、グループごとで外れ値を見たい場合は、ヒストグラムより箱ひげ図の方が簡便で便利です。
スミルノフ・グラブス検定(Grubbs’ test)
これはデータが正規分布していることが前提の統計になります。
正規分布かどうかの判定は以下のページをご覧ください!


またp<0.05のときにそのデータを外れ値となります。
何より重要なのは、Grubb’s testはデータの上限が外れ値であるかどうかを判定する検定ということです。
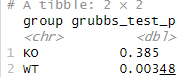
# 上限のデータが外れ値か、グループごとにスミルノフ・グラブス検定を実行し、p値を抽出
df %>%
group_by(group) %>%
summarise(
grubbs_test_p = grubbs.test(CK)$p.value # p値のみを抽出
)
# 下限のデータが外れ値か、グループごとにスミルノフ・グラブス検定を実行し、p値を抽出
df %>%
group_by(group) %>%
summarise(
grubbs_test_p = grubbs.test(CK, opposite = TRUE)$p.value # p値のみを抽出
)

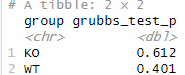

以上から、WT群では上限の値が統計的に外れ値であることが判定されました。



統計的に外れ値か判定する方法を学んだのだ!



最もやってはいけないのは、データが不都合やから統計的に検定して、除外することやで!
これは恣意的なデータの調整だから、真実の捻じ曲げにつながるからやってはならないやでな!



え、でも、指導教官がやれと・・・



その場合は仕方ないネ。上司のいうことは絶対ネ。自分が偉くなったときに正しい指導法をするネ。
まとめ
外れ値について、実際の統計手法を含めて解説しました!
少しでもお役に立てれば幸いです!!










コメント