【初心者向け】散布図・相関グラフとPearson・SpearmanのRでの使い方

2024年8月3日2024年8月6日

URLをコピーしました！

こんにちは。ほしのはやしです。
散布図・相関図はデータを見るのにとても便利な手法ですね。
このページではRを用いた散布図の書き方・統計について解説していきます！

散布図・相関と読み方

散布図とは

散布図とは、身長と体重など数値をX軸・Y軸に点で表現（プロット）した図のことです。

散布図を用いることで、２つのグループに関連性があるかどうか調べたり、他の影響を受けていそうか想像するのに役立ちます。

具体的には下記のような図を作成し理解することが本ページの目標になります！

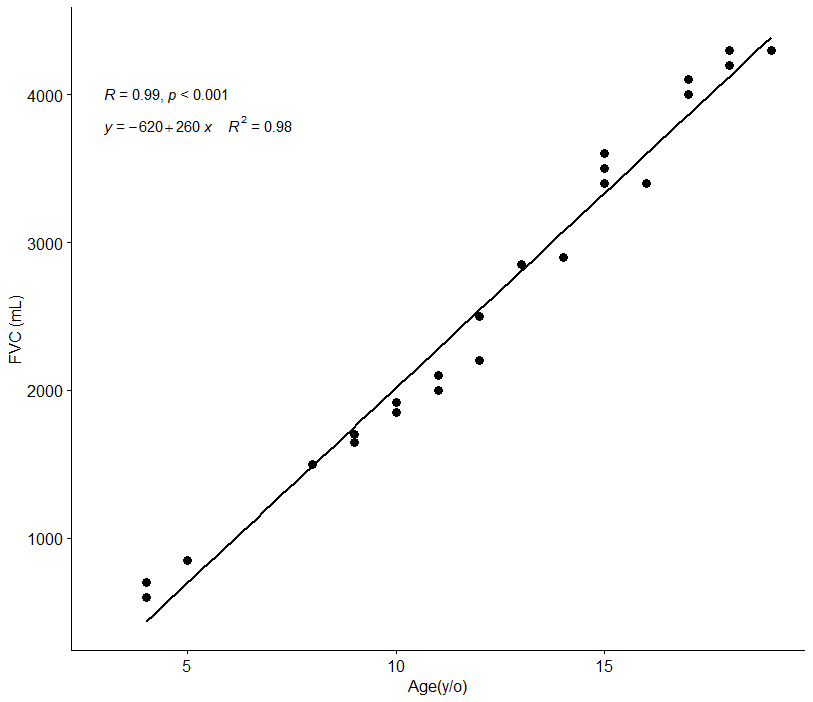
この図では、X軸が年齢、Y軸に努力性肺活量(FVC)をプロットしています。
左上にある数値（R = 0.99, p < 0.001, y = -620 +260x, R² = 0.98）が統計結果になります。

R：相関係数
p：P値
数式：回帰直線の一次関数
R²：決定係数

どの数値も大事なものなので特にこだわりがなければ全部表記しておいて大きな問題はありません。

相関係数とは～強い・弱いの基準

相関の強さを表す指標で-1から1の範囲の数値を取ります。
正の数値の場合は正の相関、負の数値の場合は負の相関といいます。

相関が強い、弱いという基準は諸説ありますが以下が俗説的な基準になります。

|R| = 0.7以上：非常に強い相関
|R| = 0.4-0.7：強い相関
|R| = 0.2-0.4：弱い相関
|R| = 0.2未満：相関なし

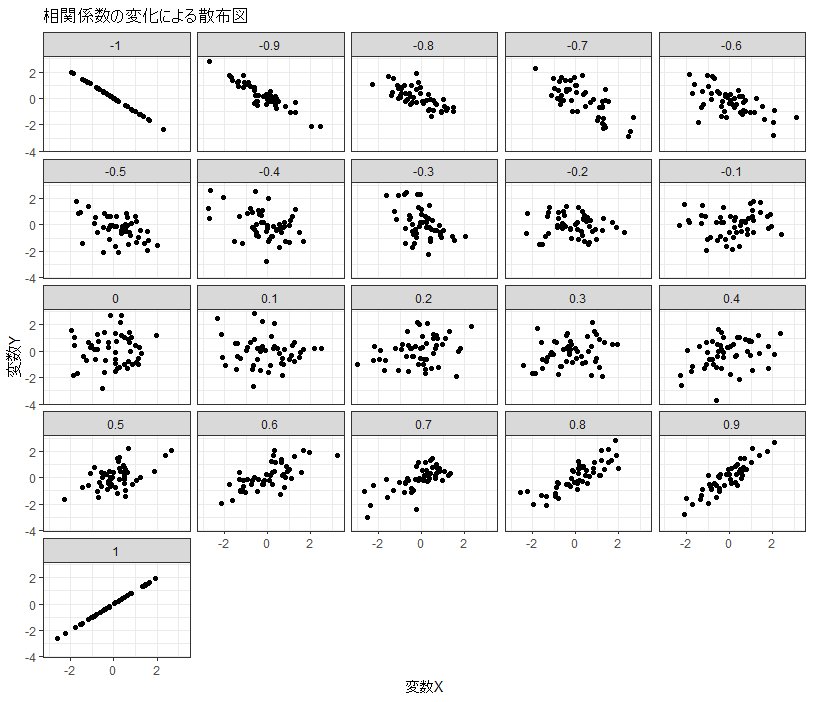
具体的には以下のような図がイメージしやすいかもしれません。

相関係数におけるP値～pearson, spearmanの選び方

まず第一に、相関係数の数値とP値は別のものだということがとても大事です。

相関係数が1や-1に近いからP値は有意になるとは言えず、逆に相関係数が小さいからP値は有意になりにくい、というのは間違っているということになります。

P値は他の統計手法と同様にN数(サンプル数)によって大きく影響されます！
P値が有意ではないからといって相関がないとは言えない、という理解が重要です。

統計手法はpearsonとspearmanの２つを覚えておけばよいでしょう。

pearson：X軸のデータ、Y軸のデータともに正規分布している場合に使えます。
spearman：正規分布していない場合も使えます。

正規分布の検定はこちらのページを参考にしてください。

決定係数とは

一次関数の数式で表された回帰直線、これの精度を表したものと考えるのが最も容易です。

0から1の範囲を取り、１に近いほど数式のモデルの精度が高いといえます。

これをもとに先ほどの図の統計（R = 0.99, p < 0.001, y = -620 +260x, R² = 0.98）を解釈すれば・・・

非常に強い正の相関が統計的な有意差を以てあり、決定係数も１に近いので、年齢がFVCに対して非常に大きな要素になると考えられる。

このような形になります。

Rでの相関グラフの書き方

具体的なコード（R studio）

ggpubrというパッケージをインストールしておいてください。
パッケージのインストール方法はこちら！

あわせて読みたい

【初心者向け】R studioの絶対必須パッケージ！導入方法も！こんにちは。ほしのはやしです。R studioをインストールしたけれど、使い方がわからない…。そんなあなたのための、パッケージ解説紹介ページです。 R studioは、パッケ…

テーブル名：data1

Age	FVC
12	2500
4	700
8	1500
15	3600
18	4200
16	3400
…	…

基本の構文は以下になります！
ggscatter(データシート名, x=”列名1“, y=”列名2“, add=”reg.line”)+
stat_cor(method=”spearman”)+
stat_regline_equation()

library(ggpubr)

ggscatter(data1, x="Age", y="FVC", size = 3, add="reg.line",xlab = "Age (y/o)", ylab = "FVC (mL)")+
    stat_cor(method = "spearman", r.accuracy = 0.01, p.accuracy = 0.001, label.x = 3, label.y = 4000)+
    stat_regline_equation(
        aes(label = paste(..eq.label.., ..rr.label.., sep = "~~~~")), 
        label.x = 3, label.y = 3800)

コードを説明していきます。

ggscatter()：
size = 3で点の大きさを調整して、xlab, ylabでそれぞれX軸, Y軸の名前を変更しています。
add=”reg.line”で回帰直線を描写しています。

stat_cor()：
method = “spearman”でspearman検定を選択しています。他には“pearson”や”kendall”に変更することができます。
r.accuracy = 0.01で相関係数Rを小数点第２位まで表示するようにしています。
p.accuracy = 0.001でP値を小数点第３値まで表示するようにしています。
label.x = 3, label.y = 4000で統計結果の表示場所をX軸で３のところ、Y軸で4000のところと設定しています。

stat_regline_equation()：
aes(label = paste(..eq.label.., ..rr.label.., sep = “~~~~”))で、決定係数R²と回帰直線の数式を表示しています。
label.x = 3, label.y = 3800で統計結果の表示場所をX軸で３のところ、Y軸で3800のところと設定しています。

これでグラフも統計も一発で完成できましたね！

散布図と外れ値

外れ値とは

グラフの書き方はマスターされたと思いますので、次は解釈について解説していきます。
よくあるのが下記のグラフのような場合…

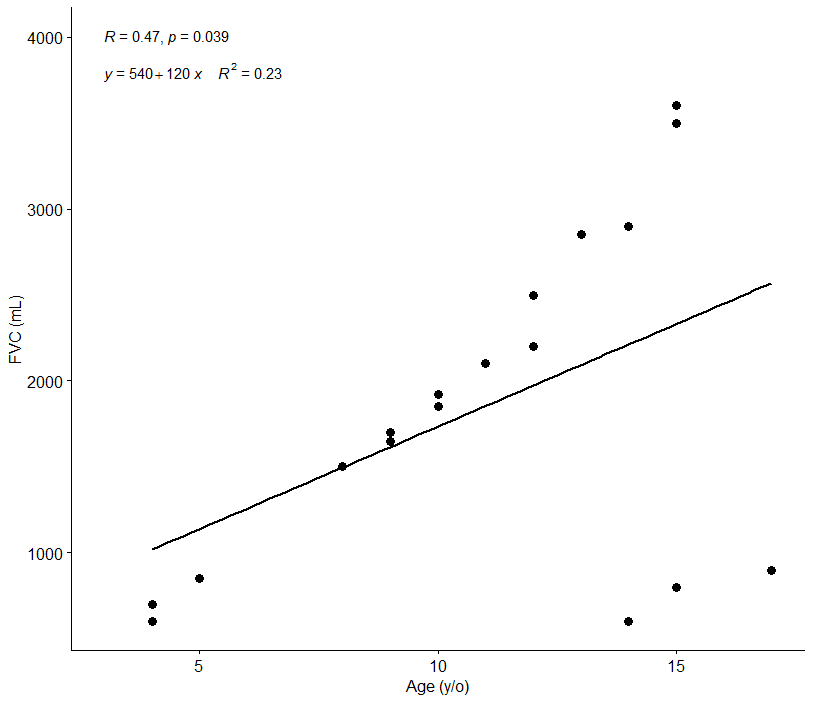
統計的に有意ではありますが、相関係数Rが0.47, 決定係数R²が0.23、でありモデルの精度が著しく落ちています。

散布図において大事なことは点の分布から違和感を感じることです。

このデータの場合、赤円で囲んだ数値がなければもっと精度が良く相関も非常に強い結果になることが予想されますね。

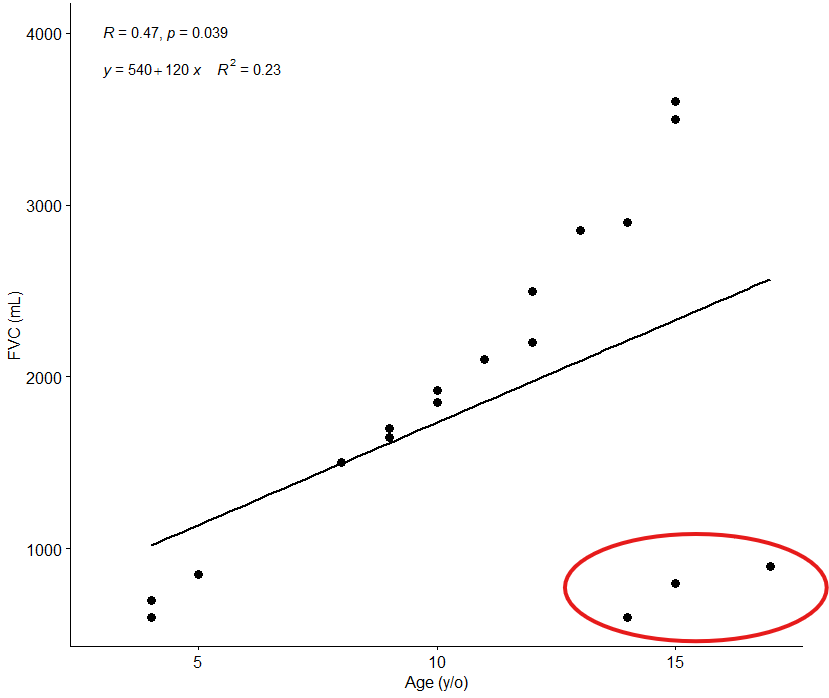
このような点のことを外れ値と呼びます。

実際に外れ値かどうかを確認するためにまずすべきことは…生データが正しいかどうかチェックすることです。

このデータの生データを確認すると、年齢が4歳, 5歳, 7歳とすべきところが14歳, 15歳, 17歳と入力されていることがわかりました。

星柴くん

外れ値と思ったら誤った入力だったんだ…

黒星柴くん

よくあることだから一番最初に気をつけるのだよ

外れ値の判定

誤ったデータではなく、実際にその数値が正しい場合、本当に外れ値として扱うかどうか難しいですよね。

そのデータが真実の可能性もありますから非常に悩みます。
ただ色々な背景からやはり外れ値として扱うのが妥当と考えられるのであれば、統計的な根拠を以て外れ値であることを主張する必要があります。

外れ値の判定には以下の方法が提唱されています。

箱ヒゲ図のヒゲの外にあるデータ
データの平均値から標準偏差が2倍以上離れているデータ
Smirnov-Grubbs（スミルノフ・グラブス）検定
クラスター分析

最も簡単な方法は箱ヒゲ図を書くことです。

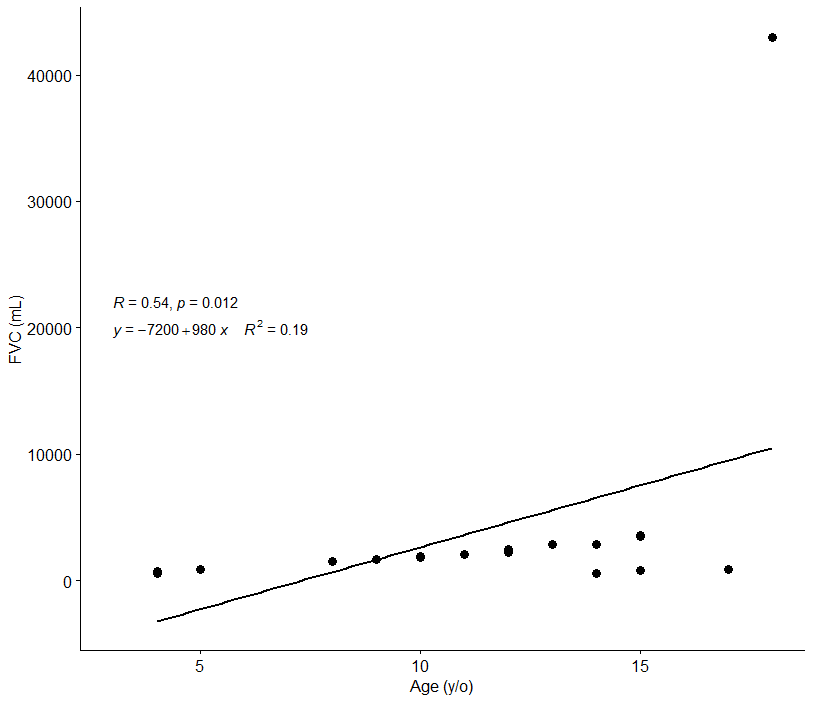
右上の点が明らかに外れ値っぽいですが、FVCの値で箱ひげ図を書いてみましょう。

boxplot(data1$FVC)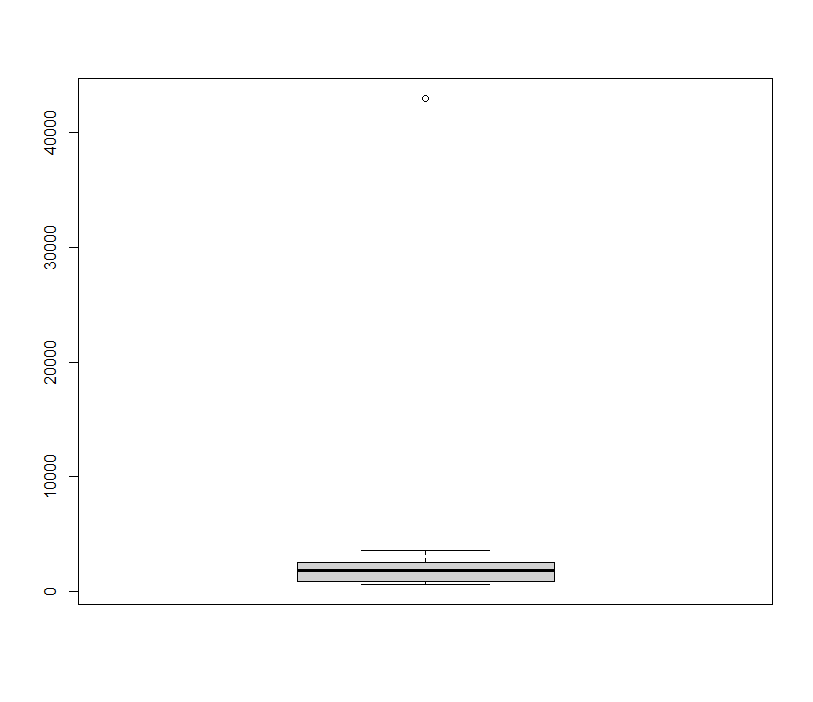

このように上のヒゲと下のヒゲの範囲外にある点のデータを外れ値として扱う、のが最も鑑別で一般的な方法です。

Smirnov-Grubbs（スミルノフ・グラブス）検定
正規分布に従うデータで、最大値または最小値が外れ値かどうかを判定する検定の一種。
データセットに一つだけ外れ値が存在すると考えられる場合に有効。
※正規分布ではない場合、複数の外れ値がある場合には適さない検定です。

install.packages(“outliers”)
library(outliers)
grubbs.test(data1$FVC)

これでP値が0.05未満の場合、最大値または最小値が外れ値と判定することができます。