こんにちは。ほしのはやしです。
多変量解析の3大手法は、重回帰分析・ロジスティック回帰分析・Cox比例ハザードですね!
このページではCox比例ハザードモデルによる分析方法について具体例を説明します。
他の統計手法については下記をご確認ください。
Cox比例ハザードモデル:Cox proportional hazard modelとは?
生存時間(イベントまでの発生時間)に影響を及ぼす因子について解析したい!
そんなときに使える統計手法になります。
よくあるパターンで説明します。
偶発的に冠動脈狭窄が90%であった患者で、3年のフォローアップの間に心筋梗塞を発症する因子を探索したい。
因子には、年齢、性別、降圧薬、心機能、狭窄発見時の採血で得られた新規タンパク質X、を想定し、それぞれの影響を多変量解析で評価したい。
抗がん剤Xを使用することで全生存期間にlog-rank検定で差が出ました。
治療効果には、年齢、性別、PS、脳転移、遺伝子変異の種類が影響する可能性があります。
どういう背景の患者がより抗がん剤Xが効きやすいかサブ解析したい。
Cox比例ハザードモデルで解析すれば、どの因子がどれぐらい効果を及ぼしやすいかをハザード比で評価することができます。
ハザード比は介入群(新薬群など)を分子、コントロール群を分母とすることがほとんどで、1より小さければ介入群によってイベントが発生しない(全生存期間解析なら予後良好)、1より大きければ介入群によってイベントが増加(全生存期間解析なら予後不良)、という解釈になります。
ロジスティック回帰と似ている部分がありますが、Cox比例ハザードモデルでは時間軸を含むことが大きな違いです!
Cox比例ハザードモデルを利用するための前提条件は?
論文では言及されていないことも多いですが、「比例ハザード性」が必要とされています。
比例ハザード性とは「どの時間で見ても、2群間のハザード比が同じ」。
すなわち、カプランマイヤー曲線で見た場合に2つの曲線が時間とともに徐々に離れていくような関係であることが必須とされています。
以下のパターンのときは、注意が必要です。
- Early effect:最初に差が出てその後並行なグラフ
- Delayed effect:最初は差がないが、あとから突然差が出てくるグラフ
- Diminished effect:最初は差があるも、その後徐々に差が縮まるグラフ
3以外のパターンでは、Cox比例ハザードモデルが使われていることが多く、また比例ハザード性の有無はカプランマイヤー曲線の見た目で判断されることが多いです。
 星柴くん
星柴くんCox比例ハザードモデルとカプランマイヤー曲線はセットでデータを出すことを覚えておこうね!
具体的なコード(R studio)
本来ならばカプランマイヤー曲線を書いて比例ハザード性を見た上で解析すべきですが、手法に集中するため架空のデータで解説します。
カプランマイヤーの説明はこちら!


テーブル名:datasheet1
| Age | Sex | PFS_time | PFS_censore | Stage | Intervention |
|---|---|---|---|---|---|
| 65 | M | 78 | 1 | I | Placebo |
| 70 | F | 80 | 1 | IV | DrugA |
| 62 | M | 145 | 0 | II | DrugA |
| 81 | M | 50 | 1 | III | DrugA |
| 76 | F | 55 | 1 | I | Placebo |
| 77 | F | 123 | 1 | IV | Placebo |
| … | … | … | … | … |
library(survival)
cox1 <- coxph(Surv(PFS_time, PFS_censore) ~ Intervention+Age+Sex, datasheet1)
summary(cox1)


今回もtbl_summaryを使って見慣れた形にしてしまいましょう!
gtsummaryのパッケージが必要なのでインストールがまだな人は下記ページを参考にしてください!


library(survival)
library(gtsummary)
cox1 <- coxph(Surv(PFS_time, PFS_censore) ~ Intervention+Age+Sex, datasheet1)
tbl_regression(cox1, exponentiate = TRUE)
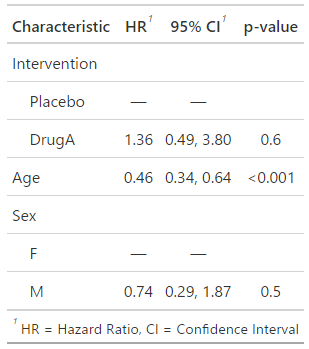

簡単にハザード比を調べることができました!
まとめ
Cox比例ハザードモデルの具体的な手法について説明しました!
少しでもお役に立てれば幸いです!










コメント