こんにちは。ほしのはやしです。
ROC曲線はよく見るものの、実際使うとなるとよく理解していないこと、ありますよね。
このページではR stusioでのROC曲線の書き方と使い方について解説します!
ROC曲線の基本
ROC曲線の由来(感度・特異度・偽陽性)
Receiver Operating Characteristic (ROC)と言われ、元来は信号処理として開発されましたが、現在は臨床検査・機械学習モデルなどの性能を評価するために利用されています。
 星柴くん
星柴くんある検査やモデルを用いて結果を予測できるようになったけど、古いものと新しいものどっちがいいのかな?



ROC曲線で視覚的にしたらわかりやすいのだ!
下の図の場合、赤の方が青よりも性能が高い!
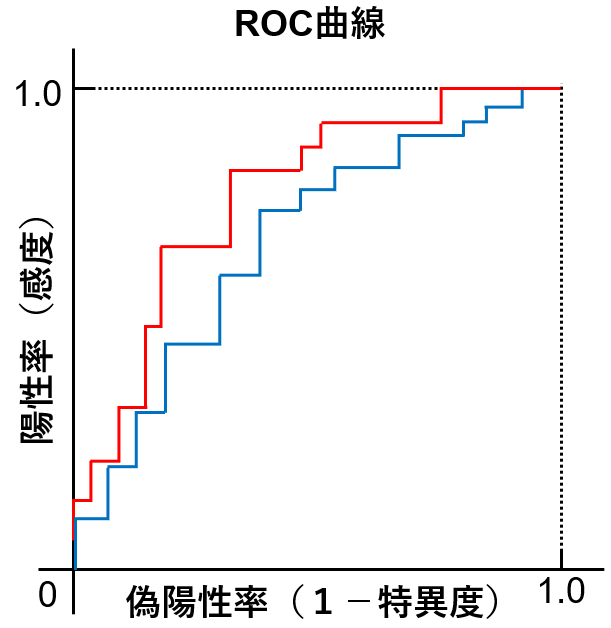

ROC曲線は、縦軸に『感度』(陽性率)、横軸に『1-特異度』(偽陽性率)で表現します。
AUC(Area Under the Curve)とは
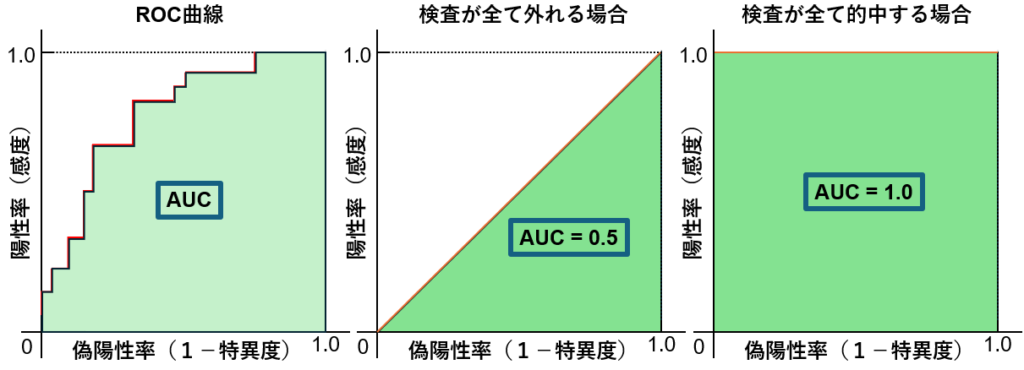
AUCとは、ROC曲線において下記の図で表される面積のことです。
検査やモデルの性能を0.5(全て外れる)~1(全て当たる)で評価しています。

ROC曲線が必要または有用な状況
以下の例のような場合にROC曲線は有用です。
- 検査やモデルのカットオフ値を決めたい
- 検査やモデルの比較をしたい
例えば、心筋梗塞に対してPCIをしたあとの、30日以内のDressler症候群の発症を予測する因子として、新規検査値Factor Xのカットオフ値を決めたい、ときに有用です。
また新規スコアリングモデルを作成したときに、既存の検査と比べて診断率や予後予測が優れているかどうかの比較検討にも使えます。
多くの論文では、Test cohort、Validation cohortのデータセットを用いて、まずはTest cohortでカットオフ値を設定し、Validation cohortでAUCを評価するということが一般的です。
ROC曲線における注意点
ROC曲線は性能評価に非常に有用ですが、注意すべき点があります。
データが不均衡(そもそもの陽性率がめちゃくちゃ低いなど)の場合は、見かけ上ROC曲線がとても良い結果に見えてしまいます。
ROC曲線は、陰性の結果が本当の陰性であること、陽性の結果が本当の陽性であること、の総和の性能を示しているので、陰性の結果自体が非常に多い場合、陰性の結果が本当の陰性であることが大多数になり、性能が良いと間違って解釈される可能性があります。
この場合は、ROC曲線ではなく、PR曲線を用いた方がよいとされています。
R studioでのROC曲線の書き方
具体的なコード(R studio)
最もよく使われるpROCというパッケージをインストールしておいてください。
パッケージのインストール方法はこちら!


テーブル名:datasheet1
| Age | Troponin | CK | CKMB | Pscore | Dressler |
|---|---|---|---|---|---|
| 63 | 0.42 | 550 | 300 | 8 | Y |
| 54 | 0.11 | 450 | 250 | 2 | N |
| 58 | 0.15 | 700 | 350 | 5 | Y |
| 72 | 0.32 | 900 | 280 | 6 | Y |
| 87 | 0.13 | 800 | 120 | 1 | N |
| 68 | 0.28 | 1200 | 450 | 3 | N |
| 44 | 0.33 | 400 | 80 | 7 | Y |
| … | … | … | … | … | … |
library(pROC)
roc_res <- roc(Dressler ~ Age + Troponin + CK + CKMB + Pscore, datasheet1, ci=TRUE)
roc_res【結果】
$Age Call: roc.formula(formula = Dressler ~ Age, data = datasheet1, ci = TRUE)
Data: Age in 25 controls (Dressler N) > 20 cases (Dressler Y).
Area under the curve: 0.473
95%CI: 0.2988-0.6472 (DeLong)
$Troponin Call: roc.formula(formula = Dressler ~ Troponin, data = datasheet1, ci = TRUE)
Data: Troponin in 25 controls (Dressler N) < 20 cases (Dressler Y).
Area under the curve: 0.611
95%CI: 0.4433-0.7787 (DeLong)
$CK Call: roc.formula(formula = Dressler ~ CK, data = datasheet1, ci = TRUE)
Data: CK in 25 controls (Dressler N) > 20 cases (Dressler Y).
Area under the curve: 0.508
95%CI: 0.3209-0.6951 (DeLong)
$CKMB Call: roc.formula(formula = Dressler ~ CKMB, data = datasheet1, ci = TRUE)
Data: CKMB in 25 controls (Dressler N) < 20 cases (Dressler Y).
Area under the curve: 0.574
95%CI: 0.4008-0.7472 (DeLong)
$Pscore Call: roc.formula(formula = Dressler ~ Pscore, data = datasheet1, ci = TRUE)
Data: Pscore in 25 controls (Dressler N) > 20 cases (Dressler Y).
Area under the curve: 0.525
95% CI: 0.35-0.7 (DeLong)
このような形で、一気にAUCと95%CIを得ることができます!
ROC曲線の書き方
同じデータセットを用いてグラフを描いていきましょう!
パッケージはpROC、ggplot2、tidyverseが必要です。
library(pROC)
library(ggplot2)
#ROCのデータを作成
roc_res <- roc(Dressler ~ Age + Troponin + CK + CKMB + Pscore, datasheet1, ci=TRUE)
#ROC曲線を描画
ggroc(roc_res, size = 1, legacy.axes = TRUE) +
geom_abline(color = "dark grey", size = 0.5) +
theme_classic()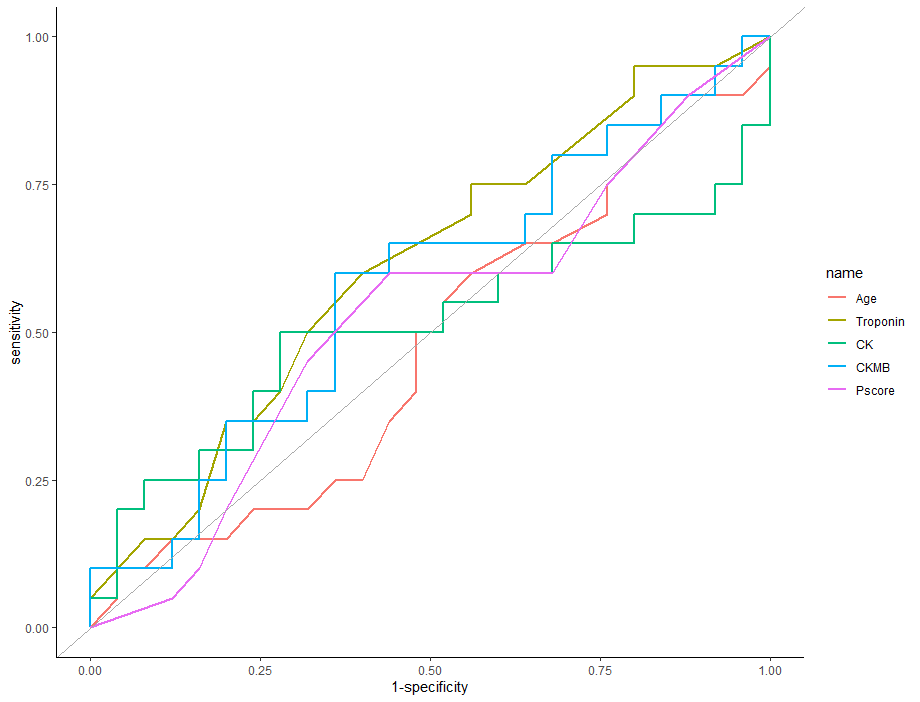

このような形でグラフが描けますが、AUCの値の表示は自由が効かないため、イラストレーターやパワーポイントにグラフを貼り付けたあとに追記するのが最も労力が少なくてすみます。
複数のROC曲線の比較
今回のデータセットでは見た目からも差はなさそうですが、AUCの値に差があるか統計的に評価してみましょう!
ROC曲線が複数ある場合、一気に比較する方法はありません。また3つ以上の検討では多重性の問題があるため最終的にはFDR調整が必要になります。
ROC曲線を複数比較する場合は、基準となるreferenceを定めて、それと比較することが基本となります!
よって、1つずつの比較の方法について説明します。
roc1 <- roc(Dressler~Age, datasheet1)
roc2 <- roc(Dressler~Troponin, datasheet1)
roc.test(roc1, roc2, method="delong")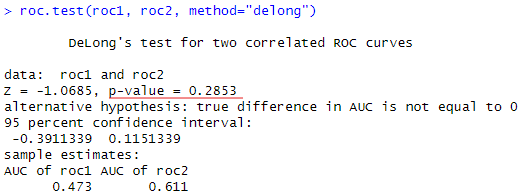

このような形でp値が出力されました!
複数繰り返す場合は、一つずつ比較していきましょう。
ROC曲線からカットオフ値の決定
検査やモデルのカットオフ値を決めるのは、現場に応じた判断が最終的には求められます。
現実的には感度・特異度はトレードオフであり両立させることは困難です。
除外を求めていくのか、特定を求めていくのか、社会的状況によって変化します。
例:COVID-19初期流行のときはできる限り感度が高いカットオフが求められ、2024年時点の蔓延状況では特異度が高いカットオフが求められます。
その中でも、検査・モデルとしてこの値が感度・特異度ともにバランスが取れているカットオフ値というものがあります。
Youden indexとベストポイント法が最もよく知られていますが、このページでは最もバランスが取れているとされるYouden indexの解析の方法を説明します。
roc2 <- roc(Dressler~Troponin, datasheet1)
plot(roc2, identity = TRUE, print.thres = "best", print.thres.best.method = "youden", legacy.axes = TRUE)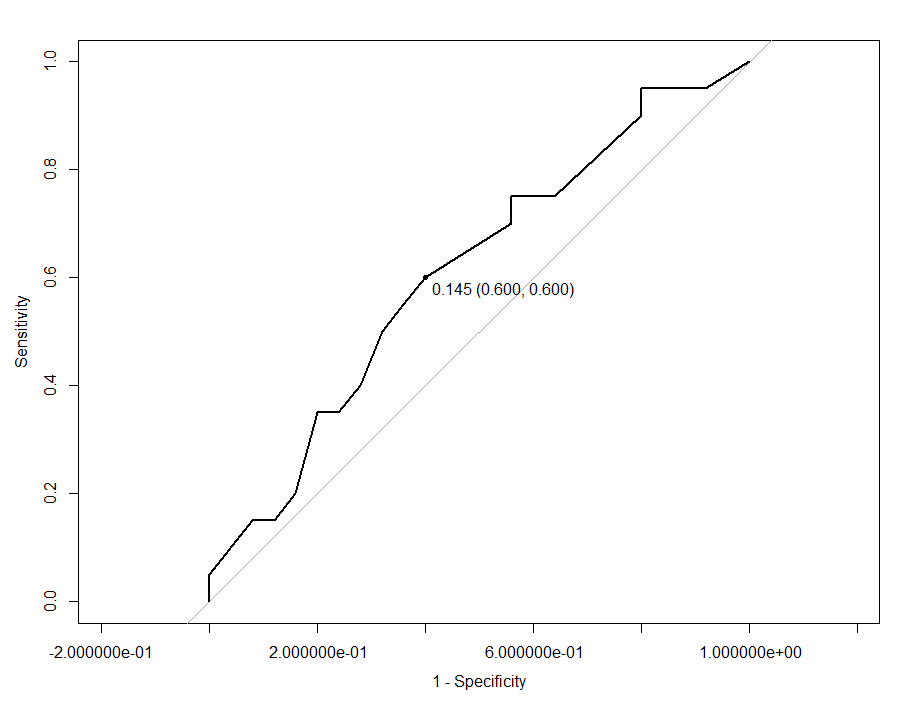

0.145 (0.600, 0.600)がYouden index(特異度, 感度)になります。
すなわちこのデータセットでは、Troponinのカットオフ値を0.145に設定した場合、特異度0.6、感度0.6の検査だと言えます。



今回の架空の研究では全然いい結果が出なかったね…



研究なんてそんなものだから、コツコツ続けるしかないのだ!
まとめ
ROC曲線をR studioで検討する方法について説明しました!
皆様のお役に立てれば幸いです!










コメント