「1要因のみ対応がある2群」の3条件以上を解析する：線形混合効果モデルの具体例

こんにちは。ほしのはやしです。

実験系でも検証(臨床)系でも、対応のある２群に対して複数条件で統計解析が必要になることありますよね。

なんとなくTwo-way repeated measure ANOVAを使えばよいのかなぁ、と考えますが、２つの要因すべてで対応のある時しか使えず困ることがあります。

このページでは「1要因のみ対応がある2群」において、３条件以上解析するための線形混合効果モデルの手法について説明します！

線形混合効果モデルを使いたい研究デザイン

次の研究例を考えます。

疾患群（疾患Aまたは疾患B)に対して、治療を４条件（Control, Intervention1, Intervention2, Intervention3）を行ってLDLの値を調べたい

このデザインでは以下のような理解が重要です。

疾患群（疾患A または 疾患B） は被験者間要因です。
※ 同じID（被験者）は 疾患A か 疾患B のいずれかに属し、両方を経験することはありません。

Intervention群4つ（Control, Intervention1, Intervention2, Intervention3） は被験者内要因です。
※ 同じID（被験者）は、4つの治療条件をすべて経験します。

この場合の解析の目的はこのようになります。

• 疾患群（疾患A vs 疾患B）の主効果：疾患ごとにLDLの値が異なるか？
• Intervention群の主効果：治療条件ごとにLDLの値が異なるか？
• 疾患群 × Intervention群の交互作用効果：疾患群によって治療条件の効果が異なるか？

この研究例に利用できるのが、線形混合効果モデル(LMM: Linear Mixed Effects Model)になります。

線形混合効果モデル(LMM： Linear Mixed Effects Model)の利点

個人差や群差を考慮できる

• LMMは、被験者やグループごとの違いを「ランダム効果」としてモデルに組み込むことができます。
• 例：異なる被験者が異なる基準値を持っていても、その個人差を考慮した解析が可能。

被験者内要因と被験者間要因を同時に解析できる

• 対応のあるデザイン（被験者内要因）と、グループ間比較（被験者間要因）を1つのモデルで解析可能。
• 例：疾患群（被験者間要因）と治療条件（被験者内要因）の影響を同時に解析。

欠測データに柔軟

• 一部のデータが欠けている場合でも、解析が可能。従来のANOVAでは欠測値があるとすべてのデータを無視する必要がありますが、LMMは欠測値を含むデータセットを扱えます。

データの階層構造に対応

• LMMは階層的なデータ（例えば、生徒がクラスに属し、クラスが学校に属するデータ）に適しています。
• 例：患者が病院に属しており、病院間の違いも考慮したい場合。

交互作用の解析が可能

• 主効果だけでなく、要因間の交互作用（要因Aが要因Bに与える影響）も解析可能。

線形混合効果モデル(LMM)の注意点

モデルの複雑さ

• LMMは構築が柔軟である反面、モデルが複雑になりやすい。
  • 過剰に複雑なモデルを作ると過適合（overfitting）のリスクがあります。
  • 過剰に単純化すると、重要な情報が失われる可能性もあります。

治療条件を８条件にするなど複雑なモデルの場合には特に注意が必要！

仮定の確認が必要

• LMMには以下の仮定が必要です：
  • 残差が正規分布に従う。
  • 各条件で分散が均一である（分散の均質性）。

練習用データセットの作成

ここからは実際のデータセットを用いた手法について解説していきます！

疾患が2群ある（疾患A、疾患B）マウスを複数用いて、Control、Intervention1, Intervention2, Intervention3の4条件でLDLの値に差があるか調べることを目標にします。

# tidyverse パッケージを読み込む
library(tidyverse)

# データ作成
set.seed(123) # 再現性のためのシード

data <- tibble(
    ID = rep(1:20, each = 4), # 被験者ID
    Disease = rep(c("DiseaseA", "DiseaseB"), each = 4, times = 10), # 疾患群
    Condition = rep(c("Control", "Intervention1", "Intervention2", "Intervention3"), times = 2 * 10) # 治療条件
)

# 疾患群ごとにLDL値を調整
data <- data %>%
    mutate(
        LDL = case_when(
            Disease == "DiseaseA" & Condition == "Control" ~ rnorm(n(), mean = 130, sd = 10),
            Disease == "DiseaseA" & Condition == "Intervention1" ~ rnorm(n(), mean = 120, sd = 10),
            Disease == "DiseaseA" & Condition == "Intervention2" ~ rnorm(n(), mean = 125, sd = 10),
            Disease == "DiseaseA" & Condition == "Intervention3" ~ rnorm(n(), mean = 110, sd = 10),
            Disease == "DiseaseB" & Condition == "Control" ~ rnorm(n(), mean = 140, sd = 10),
            Disease == "DiseaseB" & Condition == "Intervention1" ~ rnorm(n(), mean = 130, sd = 10),
            Disease == "DiseaseB" & Condition == "Intervention2" ~ rnorm(n(), mean = 135, sd = 10),
            Disease == "DiseaseB" & Condition == "Intervention3" ~ rnorm(n(), mean = 125, sd = 10)
        )
    )

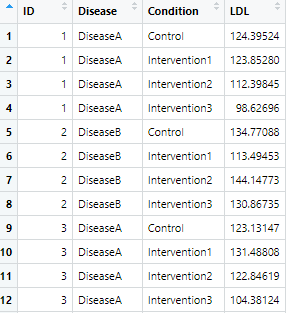
これで「長い形式」（解析に適した形）のデータセットを作成することができました！

データは基本的にこのような形式で保存するのが推奨されます。

Rで線形混合効果モデル(LMM)解析

必須パッケージの『tidyverse』『lmerTest』をインストールしておきます。
パッケージのインストール方法はこちらを参考にしてください。

あわせて読みたい

【初心者向け】R studioのおすすめパッケージとインストール方法 こんにちは。ほしのはやしです。R studioをインストールしたけれど、その後どうすればよいか途方にくれてしまうことありますよね。 特にRを使い始めたばかりの初心者に…

# lmerTest パッケージを読み込む
library(lmerTest)

# 線形混合効果モデルの構築
model <- lmer(LDL ~ Disease * Condition + (1 | ID), data = data)

# モデルの要約を確認
summary(model)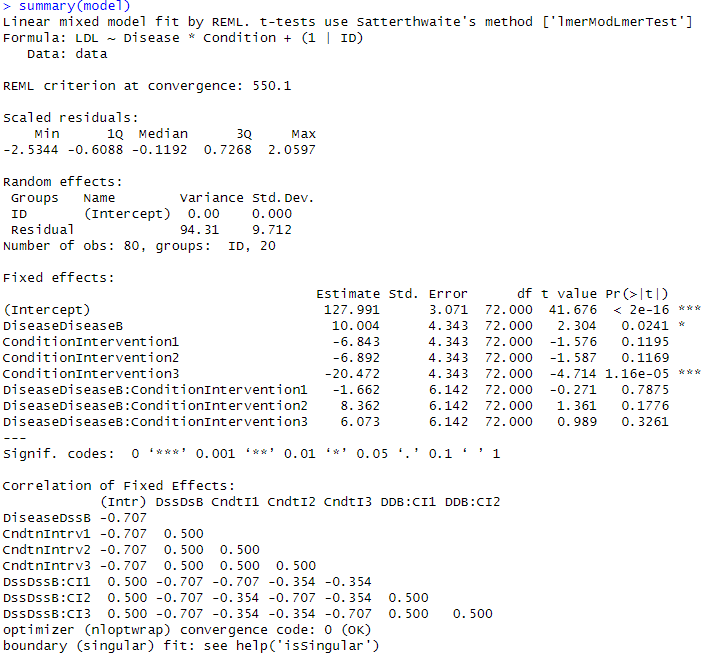

線形混合効果モデル(LMM)の結果の読み方

ランダム効果（ID)

今回はID（個体差）をランダム効果として計算しました。
結果の解釈は以下のとおりです。

• 分散が0（Variance: 0.00）となっており、被験者間でのLDL値の差がほとんどないか、モデルが適切にそのばらつきを捉えていない可能性があります。

残差（Residual)

【残差（Residual）】
分散（Variance）: 94.31
標準偏差（Std.Dev.）: 9.712

分散: 94.31

• 残差の分散は、データのばらつきの平均的な広がり（分布の広がり）を示します。
• 数値が大きいほど、モデルが説明できなかったばらつきが大きいことを意味します。

標準偏差（Std.Dev.）: 9.712

• 残差の分散の平方根を取った値で、ばらつきの平均的な大きさを示します。
• 解釈: 残差の平均的なばらつきは約9.7単位です。これは、観測されたLDL値がモデルで予測された値から、平均して±9.7程度ずれることを意味します。

残差とは？

残差は、実際の観測値とモデルが予測した値（適合値）の差です。
残差が小さいほど、モデルが観測データをよく説明していることを意味します

この結果からわかること

今回のモデルでの残差の分散が94.31というのは、残差（予測値と観測値の差）のばらつきが比較的大きいことを示しています。つまり、モデルが予測した値と実際の値にはある程度の違いがあり、それが平均して94.31の分散を持つことになります。

LDL値は、個々の条件や疾患群の違いだけでなく、他の予測されていない要因によるばらつき（個体差や測定誤差など）があることを示唆しています。

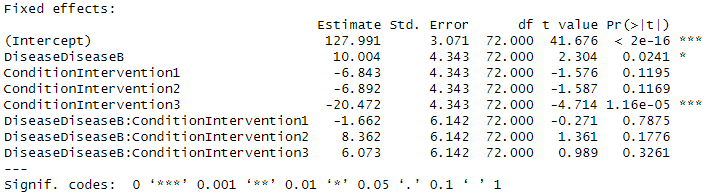
固定効果（Fixed effects）の解釈

固定効果は、基準カテゴリ（DiseaseA × Control）と比較した各効果を示します。

何を基準にするかはデータセットの順番で異なることがあります。
そのため、解析の前に以下のようにlevelsで順位付けをすることで一番左の項目が基準カテゴリーとして選ばれるようにできます！

# DiseaseとConditionの基準カテゴリを設定
data$Disease <- factor(data$Disease, levels = c(“DiseaseA”, “DiseaseB”)) data$Condition <- factor(data$Condition, levels = c(“Control”, “Intervention1”, “Intervention2”, “Intervention3”))

基準カテゴリ（Intercept）

• 推定値: 127.991
  • DiseaseA かつ Controlの条件における平均LDL値。
• p値: < 2e-16（非常に有意）
  • 基準値（ゼロ）と比較して、DiseaseAかつControlの条件の平均LDL値が統計的に有意に異なることを示します。

主効果

Disease（疾患群）:

DiseaseDiseaseB: 10.004

• DiseaseBのLDL値はDiseaseAより約10単位高い。
• p値: 0.0241（有意、p < 0.05）
• 解釈: DiseaseBのLDL値はDiseaseAに比べて有意に高い。

Condition（治療条件）:

ConditionIntervention1: -6.843

• Intervention1のLDL値はControlより約6.8単位低い。
• p値: 0.1195（有意ではない）

ConditionIntervention3: -20.472

• Intervention3のLDL値はControlより約20.5単位低い。
• p値: 1.16e-05（非常に有意、p < 0.001）
• 解釈: Intervention3はLDL値を有意に低下させる。

交互作用

Disease × Conditionの交互作用項:

• すべての交互作用効果のp値が0.05より大きい。
• 解釈: 疾患群と治療条件の間に明確な相互作用効果は観察されなかった。

結論

• DiseaseBはDiseaseAに比べて有意に高いLDL値を持つ。
• Intervention3はLDL値を有意に低下させる。
• 疾患群と治療条件の間の交互作用効果は明確ではない。

Post-hoc解析

パッケージ『emmeans』をインストールしておいてください。

library(emmeans)

emm <- emmeans(model, pairwise ~ Disease * Condition, adjust = "tukey")
pairs(emm, simple = "each")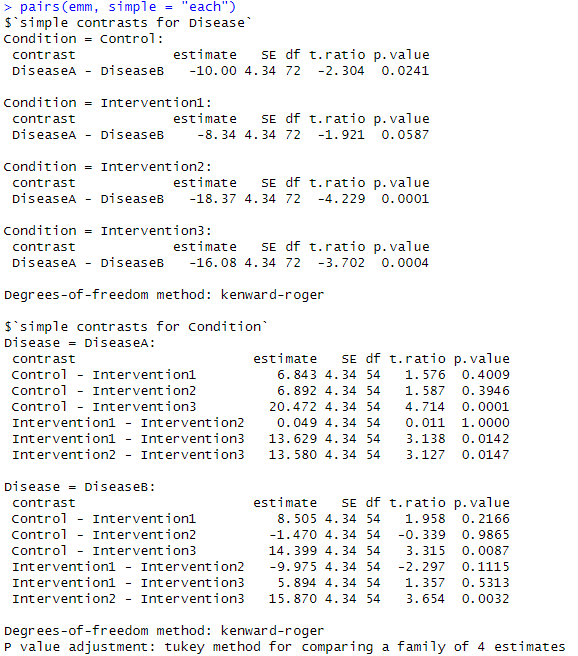

事後解析でどことどこに差があるか明確になりましたね！

まとめ

線形混合効果モデルが適応できる研究デザイン、利点・注意点、使用方法の具体例について解説しました！
少しでもお役に立てたなら幸いです！