こんにちは。ほしのはやしです。
3群以上での対応のある場合にどのようにすればよいか、結構悩みますよね。
このページではRを使った具体的な統計の方法、およびグラフの作成について解説します!
まず最初に多重性調整について理解を共有します!!
多重性調整(Multiple Testing Correction)とは?
多重性調整(または多重比較の調整)は、統計解析において非常に重要です。
特に、複数のグループを比較する場合に、誤った結論を避けるために欠かせない知識になります。
まず最初に、なぜ多重性調整が必要なのか、そしてその仕組みについてわかりやすく解説します。
多重性とは?
「多重性」とは、複数の統計的検定を行うこと、または繰り返し行うこと、を指します。
例えば、3つ以上の異なる治療法(グループ)を比較する場合、各グループをペアごとに比較する必要があります。
この場合、2つ以上の統計検定(例えば、t検定やWilcoxon検定)を行うことになります。
複数の検定を行うと、『偶然による誤った結果(偽陽性)』が出る確率が高くなります。
つまり、実際には差がないのに、統計的に有意だと誤って判断してしまう可能性が増えるのです。
偽陽性のリスク
統計的な検定では、「p値」という数値が重要です。
p値は、帰無仮説(差がない、または効果がないという仮定)が正しい場合に、観測されたデータがどれくらい珍しいかを示します。
通常、p値が0.05未満であれば、差が有意であると判断します。
しかし、複数回の検定を行うと、偶然によってp値が0.05未満になる確率が高くなります。
これがいわゆる偽陽性(差がないのに差があると誤って結論する)です。
多重性調整の必要性
複数の検定を行う場合、多重性調整を行うことで、偽陽性のリスクをコントロールします。
調整を行わないと、実際には差がない場合でも、偶然の偏りで統計的に有意だと判定してしまうことがあるからです。
多重性調整の方法
多重性調整にはいくつかの方法があり、代表的な方法を紹介します。
- ボンフェローニ補正(Bonferroni correction)
ボンフェローニ補正は、最も単純な調整方法です。各p値を検定の回数で割って、新しい閾値を設定します。これにより、複数回の検定で偽陽性が出るリスクを抑えます。例えば、5回検定を行う場合、p値が0.05未満であれば有意とする代わりに、各p値を0.05÷5=0.01とすることで、より厳密な基準が適用されます。 - ホルム補正(Holm correction)
ホルム補正は、ボンフェローニ補正を少し改良した方法です。p値を小さい順に並べて、順番に調整を行います。ボンフェローニ補正よりも効率的であり、偽陽性を抑える効果が高いです。 - FDR補正(False Discovery Rate)
FDR補正(偽発見率補正)は、特に多くの検定を行う場合に使用されます。偽陽性の割合を制御する方法で、ボンフェローニ補正よりも柔軟であり、検定数が多い場合に有効です。
実験系やSNPs系の論文ではホルム法を使っておいたらまず大丈夫です
実際の例:多重性調整を行う理由
例えば、治療法を3つ比較する場合、以下の3つの比較が行われます:
- 治療法A vs 治療法B
- 治療法A vs 治療法C
- 治療法B vs 治療法C
これらの比較すべてで独立にt検定を行うと、それぞれにp値が出ます。
しかし、どれか1つでも偽陽性(偶然の差)が見つかる確率も高くなります。
ここで、多重性調整を行うことで、全体として偽陽性が出る確率を制御し、より信頼性のある結果を得ることができます。
 星柴くん
星柴くん学位審査やthesis defenceでよく突っ込まれるところなのだ



『多重性調整はどのようにされましたか?』『仮に多重性調整をHolm法でした場合、有意差が見られなくなりますが、結果をどう説明しますか?』
こんな感じで学生の理解度を確認するのは頻出やでな!
練習用データの作成
細胞サンプル毎に3つの条件(Control, Intervention1, Intervention2)でタンパク質Aの濃度を測定して比較したい場合を考えます。
データシート名:Testdata
# Set seed for reproducibility
set.seed(42)
# Generate dummy data
CellName <- paste0("Cell_", 1:20)
Control <- rnorm(20, mean = 50, sd = 10) # Random values around 50
Intervention1 <- rnorm(20, mean = 120, sd = 10) # Random values around 120
Intervention2 <- rnorm(20, mean = 70, sd = 10) # Random values around 70
# Create a data frame
Testdata <- data.frame(CellName, Control, Intervention1, Intervention2)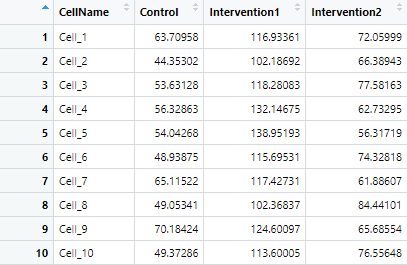

このようなデータシートを作成しました。
同じサンプルに対して複数の条件を比較する場合は「対応のあるデータ」とみなしてOK!
統計解析用に『長い形式』(Long format)に変更する
先ほどのようにデータを入力している状況を横に広がった形で『ワイド形式』と呼びます。
しかし、Rで統計解析するためにはこれを縦に『長い形式』(Long format)に変更する必要があります。
この変更とその後の解析にはパッケージに『tidyverse』と『rstatix』が必要なので、インストールしておいてください。
パッケージのインストール方法はこちらをご覧ください。


# 必要なパッケージを読み込み
library(tidyverse)
library(rstatix)
# データを長い形式に変換
Testdata_long <- Testdata %>%
pivot_longer(
cols = -CellName, # CellName以外の列を変換
names_to = "Group", # 列名を "Group" 列に変換
values_to = "ProteinA" # 各値を "ProteinA" 列に変換
)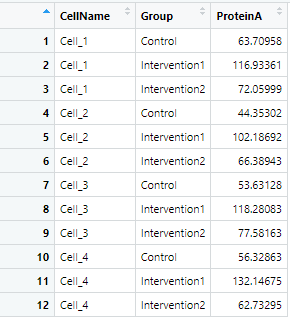

このように新しくTestdata_longというデータシートを解析用に作成しました。



そもそもデータを長い形式で保存していればこの手間を省けたのだ



複数のタンパク質を測定する場合とか、ワイド形式だと一枚のテーブルシートにまとめるのは難しいから、初めから長い形式でデータをまとめる癖を作っておくやで!
3群以上での対応のある統計解析
まずはデータが正規分布するかどうかによってt検定を行う(正規分布する)か、wilcoxon検定を行う(正規分布するか不明、サンプル数が少なくても判別不可)かを決定します。
実験系の場合はサンプル数が少ないことが多くwilxocon検定を使うのでよいでしょう。
t検定をどうしても使いたくて正規分布などを確認する方法は以下のページをご覧ください。


Wilxocon符号順位検定のコード
library(tidyverse)
library(rstatix)
# Wilcoxon 符号順位検定(多重性調整付き)
wilcoxon_results <- Testdata_long %>%
pairwise_wilcox_test(
ProteinA ~ Group,
paired = TRUE, # 対応のあるデータ
p.adjust.method = "holm" # holm法での多重性調整
)
# p値を条件に応じてフォーマット
wilcoxon_results <- wilcoxon_results %>%
mutate(
p_value_formatted = ifelse(p.adj < 0.001,
"p < 0.001", # p < 0.001 の場合
sprintf("p = %.3f", p.adj)) # それ以外は小数3桁で表示
)
view(wilcoxon_results)

最終的に出力された『wilcoxon_results』では
p:『補正されていないP値』
p.adj:『holm法で調整したP値』
p_value_formatted:『論文用にp <0.001とそれ以外は少数3桁で表示したもの』
をまとめて表示できます。
対応のあるt検定のコード
library(tidyverse)
library(rstatix)
# Paired t-test(多重性調整付き)
t_test_results <- Testdata_long %>%
pairwise_t_test(
ProteinA ~ Group,
paired = TRUE, # 対応のあるデータ
p.adjust.method = "bonferroni" # ボンフェローニ法で多重性調整
)
# p値を条件に応じてフォーマット
t_test_results <- t_test_results %>%
mutate(
p_value_formatted = ifelse(p.adj < 0.001,
"p < 0.001", # p < 0.001 の場合
sprintf("p = %.3f", p.adj)) # それ以外は小数3桁で表示
)

対応のある3群以上のグラフの描き方
基本的には箱ひげ図にドットグラフを組み合わせて、状況に応じてペアであることを示すためにドットをラインで繋ぐ方法がおすすめです。
もちろんサンプル数が多くて見にくくなる場合は、ラインをつなぐことは省いてもよいでしょう。
今回はできるだけ簡単に書くために、パッケージ『ggpubr』をインストールしておいてください。
library(ggpubr)
# ggpairedプロットの作成
ggpaired(Testdata_long,
x = "Group",
y = "ProteinA",
fill = "Group",
point.size = 3, # ポイントサイズの設定
id = "CellName", # ペアを結びつけるID (CellName)
line.color = "gray60", # 線の色
line.size = 0.5, # 線の太さ
palette = c("white", "gray60", "gray20")) + # 色の設定
# 補正したP値をグラフに書き込む
geom_signif(
data = wilcoxon_results,
aes(xmin = group1,
xmax = group2,
annotations = p_value_formatted,
y_position = c(150, 165, 155)), # p値表示位置
textsize = 6, # p値の文字サイズ
tip_length = 0.01, # 矢印の長さ
manual = TRUE # 手動配置
) +
# 軸ラベル設定
labs(x = "薬の種類",
y = "Protein A (ng/mL)") # XおよびY軸ラベル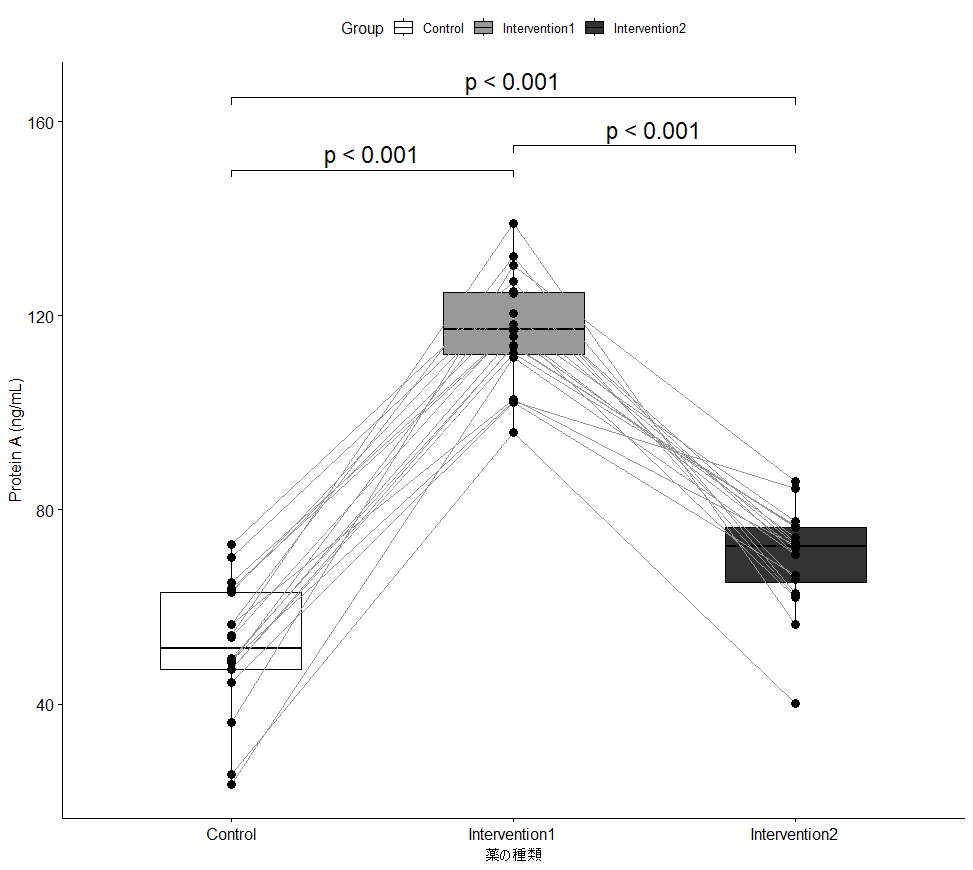

補正したP値をグラフに有意差ラインとともに付け加える方法は以下のページの最下部をご覧ください。


まとめ
多重性調整と箱ヒゲ図にドットグラフを重ねてラインでつなぐ方法を解説しました!
少しでもお役に立てれば幸いです。










コメント