こんにちは。ほしのはやしです。
対応のある2群で3条件以上でどう統計解析をしたら良いか悩みますよね。
例えば、細胞株で、低グルコース・高グルコースの育成状況を分けて、治療介入それぞれの条件でこの2群で差があるか調べたい、こんなときはtwo-way repeated measure ANOVAを使うのが良いことが多いです。
このページではTwo-way repeated measure ANOVAを主体に、統計解析・グラフの作成について解説していきます!
Two-way repeated measures ANOVA(2要因の対応のある分散分析) とは?
Two-way repeated measures ANOVA(2要因の対応のある分散分析) は、以下のようなデータを解析するための手法です:
- 2つの独立変数(要因) を持つデータを解析。
- 例えば、同じ被験者が複数の条件を受ける状況に適しています。
- 従属変数 は連続データ(例: 測定値、スコア)である必要があります。
- 主に次の3つの効果を調べることができます:
- 主効果(Main effect):各要因が従属変数に与える影響。
- 交互作用効果(Interaction effect):2つの要因が組み合わさったとき、従属変数に対して個別の要因以上の影響を及ぼすか。
例:疾患と治療条件でのLDL値解析
以下のようなデザインを考えます:
- 要因1:育成条件(LowGlc vs HighGlc)
- 要因2:治療条件(Control, Intervention1, Intervention2, Intervention3)
- 従属変数:LDL値
この統計における問い
- 育成条件によるLDL値の違いはあるか?(主効果:Culture)
- 治療条件によるLDL値の違いはあるか?(主効果:Condition)
- 疾患と治療条件が相互に影響しあっているか?(交互作用効果)
このようなことを調べたい場合にまず最初に考える統計手法になります!
Two-way Repeated Measures ANOVA の利点と注意点
利点
- 個々のサンプルが自身の対照として機能するため、データのばらつきを減らし、検出力が向上します。
- 主効果と交互作用効果を同時に検討できる。
注意点
- 仮定
- 正規性: データが正規分布に従う。
- 等分散性(または共分散の球状性): 条件間の分散が等しい。Mauchlyの検定で確認可能。
- デザインの適切性
- 要因が対応のある設計かどうか確認。
- 独立変数が完全にバランスされている必要があります(例: 各条件でデータが均等に分布)。
特に、正規性・等分散性がない場合は、他のANOVAと同様に使用できませんので、以下のページを参考に正規性・等分散性を評価するのが推奨されます。

 星柴くん
星柴くん論文では正規性・等分散性を評価困難なデータでも使用されていることがあるのだ



実験系などでデータが正規性・等分散性が担保されると想定される場合は、実際正規性などがなくても良く使用されているんやで
臨床前向き研究などの検証系の場合には、特に注意して使えるかどうか評価が必要やでな
練習用データセットの作成
ここからは実際のデータセットを用いた手法について解説していきます!
育成条件が2群ある(低グルコース、高グルコース)細胞株を複数用いて、Control、Intervention1, Intervention2, Intervention3の4条件でLDLの値に差があるか調べることを目標にします。
# tidyverse パッケージを読み込む
library(tidyverse)
# データ作成
set.seed(123) # 再現性のためのシード
data <- tibble(
ID = rep(1:10, each = 8), # 被験者ID
Culture = rep(c("LowGlc", "HighGlc"), each = 4, times = 10), # 育成条件
Condition = rep(c("Control", "Intervention1", "Intervention2", "Intervention3"), times = 2 * 10) # 治療条件
)
# 育成条件ごとにLDL値を調整
data <- data %>%
mutate(
LDL = case_when(
Culture == "LowGlc" & Condition == "Control" ~ rnorm(n(), mean = 130, sd = 10),
Culture == "LowGlc" & Condition == "Intervention1" ~ rnorm(n(), mean = 120, sd = 10),
Culture == "LowGlc" & Condition == "Intervention2" ~ rnorm(n(), mean = 125, sd = 10),
Culture == "LowGlc" & Condition == "Intervention3" ~ rnorm(n(), mean = 110, sd = 10),
Culture == "HighGlc" & Condition == "Control" ~ rnorm(n(), mean = 140, sd = 10),
Culture == "HighGlc" & Condition == "Intervention1" ~ rnorm(n(), mean = 130, sd = 10),
Culture == "HighGlc" & Condition == "Intervention2" ~ rnorm(n(), mean = 135, sd = 10),
Culture == "HighGlc" & Condition == "Intervention3" ~ rnorm(n(), mean = 125, sd = 10)
)
)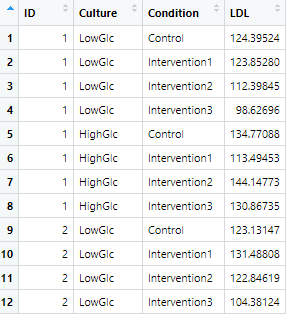

これで「長い形式」(解析に適した形)のデータセットを作成することができました!
データは基本的にこのような形式で保存するのが推奨されます。
RでTwo-way repeated measure ANOVA解析
必須パッケージの『tidyverse』『rstatix』をインストールしておきます。
パッケージのインストール方法はこちらを参考にしてください。


# 必要なパッケージを読み込む
library(tidyverse)
library(rstatix)
# Two-way repeated measures ANOVA
anova_results <- data %>%
anova_test(
dv = LDL, # 従属変数
wid = ID, # 対応の単位
within = c(Culture, Condition) # 独立変数
)
# 結果を表示
anova_results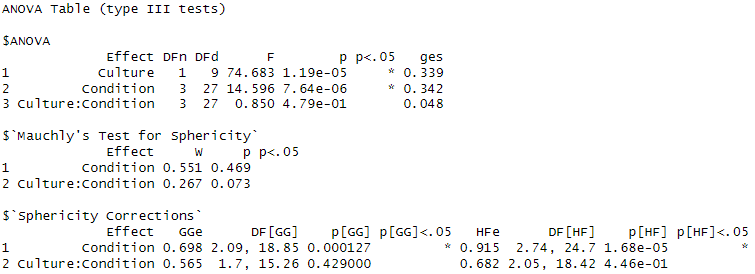

今回はデータシート名『data』、差をみたい数値の列名『LDL』、同じサンプルであることを示す列名『ID』、調べたい要因の列名1『Culture』、調べたい要因の列名2『Condition』で上記のスクリプトになっています。
Two-way repeated measure ANOVA解析の読み方
上の段落のANOVAについて、『p』と『ges』について理解すれば概ね問題ありません。
『p』がいわゆる有意差で、上から順に以下について統計評価しています。
・育成条件によるLDL値の違いはあるか?(主効果:Culture)
・治療条件によるLDL値の違いはあるか?(主効果:Condition)
・疾患と治療条件が相互に影響しあっているか?(交互作用効果)
今回の結果から以下のように解釈できます。
育成条件の影響: 育成条件がLDLに有意な影響を与えています(p < 0.001)。グルコースの状況によって治療反応が変わる可能性を示唆しています。
治療条件の影響: 4つの治療条件(Control, Intervention1, Intervention2, Intervention3)はLDL値に有意な影響を与えています(p < 0.001)。治療方法によってLDL値に顕著な差があるため、治療が効果的である可能性があります。
交互作用の影響: 育成条件と治療条件の交互作用は有意ではない(p = 0.479)。治療条件の効果は育成条件による違いに影響されないため、治療方法はグルコースに関係なく効果があると解釈できます。
『ges』とは?
GES(Generalized Eta Squared) は、ANOVAの結果を解釈する際に使用される効果量の指標で、各要因や交互作用が全体の変動にどれだけ貢献しているかを示します。GESは、特に異なる実験設計間で比較可能な効果量を提供するため、他の効果量指標(例えば、Partial eta squared)よりも広い適用範囲を持っています。
一般的に、GESの数値は0から1の間で、以下のように解釈されます:
- 0.01(小さい効果)
- 効果量が非常に小さく、要因の影響が全体の変動にほとんど寄与していないことを示します。
- 0.06(中程度の効果)
- 要因が一定の影響を与えており、全体の変動の約6%を説明していることを示します。この効果は、通常は意味があるが、非常に大きな影響とは言えません。
- 0.14(大きい効果)
- 要因が全体の変動に対してかなり大きな影響を与えていることを示し、実務的にも重要な差がある可能性を示唆します。この数値は、比較的強い実験的影響が存在する場合に見られます。
今回、Culture間、Intervention間でそれぞれ0.339、0.342とgesが大きく、グルコースおよび治療法の変更によってLDLが大きく影響するだろうと解釈できるでしょう。
Mauchly’s Test for Sphericity(球状性検定)
Mauchly’s Test は、球状性(等分散共分散の仮定)が成立しているかどうかを確認するための検定です。
両方の効果(Condition, Culture:Condition)でp値が0.05以上のため、球状性の仮定は満たされていると考えられます。つまり、分散の均等性について問題はないと判断できます。
Sphericity Corrections(球状性補正)
Conditionの結果
球状性補正後、Conditionの効果は引き続き有意(p < 0.05)です。補正後も治療条件はLDLに強い影響を与えることが確認されます。
Culture:Conditionの結果
球状性補正後、交互作用は引き続き有意ではありません(p > 0.05)。交互作用は検出されていないため、治療条件の効果が育成条件に依存しないことが再確認されます。
Post-hoc解析の実行
育成条件ごと、治療法によってLDLの値に差があることがわかりましたが、どことどこで差があるのかについては追加で解析する必要があります。
今回に限って言えば、育成条件(Culture) と 治療条件 (Condition) に関して有意な差が見られましたが、育成条件と治療条件の交互作用 (Culture:Condition) については有意差は見られませんでした(p = 0.479)。したがって、交互作用を考慮した検定結果に基づいた解釈は不要で、主効果に注目することが重要です。
Post-hoc解析の具体例
- Conditionの効果(条件間の差)について有意差が見られたため、条件間のペアワイズ比較を行うことが必要です。Bonferroni補正やHolm補正を使用して、複数の比較における誤差率を調整します。
- Cultureの効果についても有意差があるため、育成条件の間での差を検定します。
具体的には、以下のようにpairwise_t_test()を用いて、治療条件(Condition)と育成条件(Culture)の効果に対してペアワイズ比較を実行します。
まずは育成条件ごとで統計を行います。
# 各条件(LowGlc, HighGlc)で治療条件のペアワイズt検定をまとめて実行
post_hoc_condition_by_culture <- data %>%
group_by(Culture) %>% # Cultureごとにグループ化
group_split() %>% # グループごとにデータを分割
map(~ {
test_result <- pairwise_t_test(
.x, # グループごとのデータ
formula = LDL ~ Condition, # 治療条件ごとの比較
p.adjust.method = "none" # 補正は後で行う
)
# 結果にCultureを追加
test_result$Culture <- unique(.x$Culture)
return(test_result)
})
# 結果を1つのデータフレームにまとめる
culture_results <- bind_rows(post_hoc_condition_by_culture)
# 全体でp値補正
culture_results <- culture_results %>%
mutate(p.adj = p.adjust(p, method = "bonferroni")) # 全体でBonferroni補正
# 結果の表示
culture_results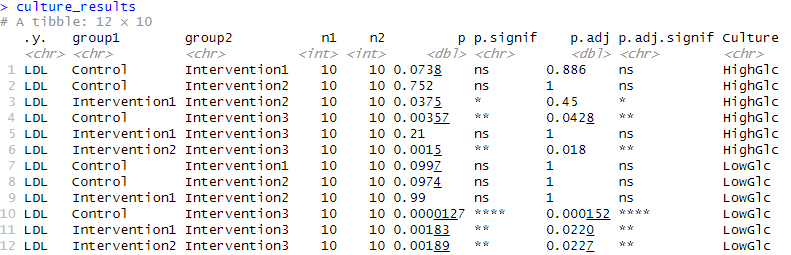

列名のpが補正する前のP値で、p.adjが補正後のP値になります!
bonferroni以外を適応する場合は、”bonferroni”を”holm”などにご変更ください。
続いて、同様に治療条件ごとで統計評価を行います。
library(tidyverse)
library(rstatix)
# 各条件(Control, Intervention1, Intervention2, Intervention3)で育成条件間のペアワイズt検定をまとめて実行
post_hoc_condition_culture_all <- data %>%
group_by(Condition) %>% # Conditionごとにグループ化
group_split() %>% # グループごとにデータを分割
map(~ {
test_result <- pairwise_t_test(
.x, # グループごとのデータ
formula = LDL ~ Culture, # 育成条件ごとの比較
p.adjust.method = "none" # 補正は後で行う
)
# 結果にConditionを追加
test_result$Condition <- unique(.x$Condition)
return(test_result)
})
# 結果を1つのデータフレームにまとめる
condition_results <- bind_rows(post_hoc_condition_culture_all)
# 全体でp値補正
condition_results <- all_results %>%
mutate(p.adj = p.adjust(p, method = "bonferroni")) # 全体でBonferroni補正
# 結果を表示
condition_results

以上で解析を一通り終了することができました!
グラフの作成
グラフの作成の前に、p値を『少数位3桁かつp<0.001はp<0.001と表記』するように調整します。
# p値のフォーマット関数
format_p_value <- function(p) {
if (p < 0.001) {
return("<0.001")
} else {
return(sprintf("= %.3f", p))
}
}
# フォーマットを適用してp値を表示し、Culture毎に位置を調整
culture_results <- culture_results %>%
mutate(
adjusted_p_value = sapply(p.adj, format_p_value), # p値のフォーマット
x1 = as.numeric(factor(group1, levels = c("Control", "Intervention1", "Intervention2", "Intervention3"))), # group1を数値化
x2 = as.numeric(factor(group2, levels = c("Control", "Intervention1", "Intervention2", "Intervention3"))), # group2を数値化
xmin = ifelse(Culture == "HighGlc", x1 - 0.2, x1 + 0.2), # HighGlcは左に、LowGlcは右に配置
xmax = ifelse(Culture == "HighGlc", x2 - 0.2, x2 + 0.2) # xminとxmaxで位置調整
)
# フォーマットを適用してp値を表示し、位置を調整
condition_results <- condition_results %>%
mutate(
adjusted_p_value = sapply(p.adj, format_p_value),
x = as.numeric(factor(Condition, levels = unique(Condition))), # x軸位置を数値に変換
xmin = x - 0.2, # xminをxから計算
xmax = x + 0.2 # xmaxをxから計算
)P値の位置を記載するのにパッケージ『ggprism』『ggpubr』が必要になるのでインストールしておいてください!
# グラフの作成
library(ggpubr)
library(ggprism)
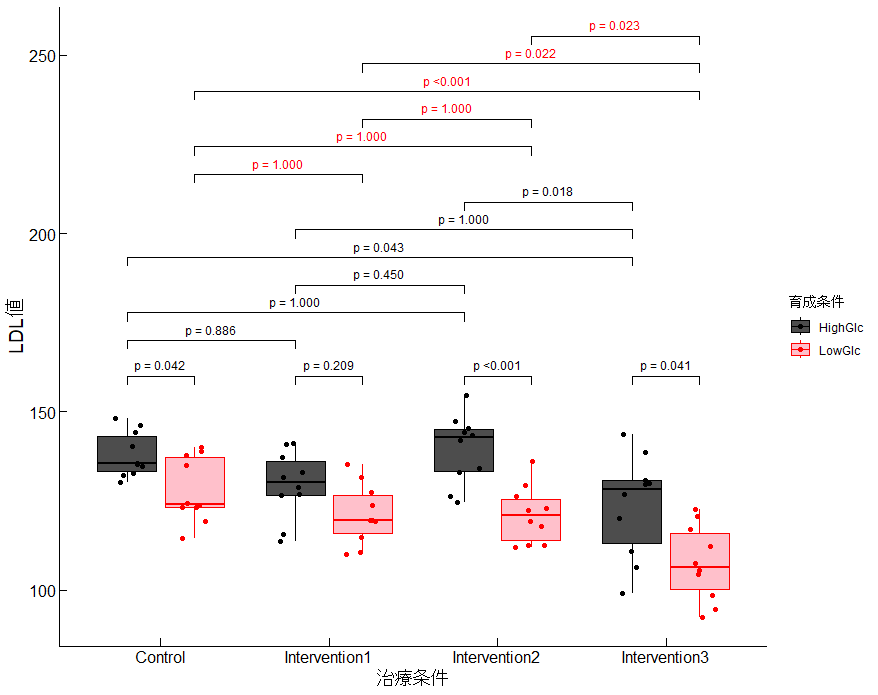
# ggboxplotを使用して箱ひげ図を作成
ggboxplot(
data,
x = "Condition", y = "LDL", color = "Culture", fill = "Culture",
add = "jitter" # ドットプロットを追加
) +
# Cultureごとの色を指定
scale_color_manual(values = c("black", "red")) + # 枠線の色
scale_fill_manual(values = c("gray30", "pink")) + # 塗りつぶしの色
# 補正したP値をグラフに書き込む(色はCulture毎で変更)
add_pvalue(
data = culture_results,
xmin = "xmin",
xmax = "xmax",
label = "p {adjusted_p_value}",
y.position = 170, # P値を記載するY軸の高さの設定
textsize = 6,
colour = "Culture", # 育成条件でP値を色分けする設定
tip_length = 0.01,
step.increase = 0.1, # P値の高さが段階的に増加するように調整
bracket.colour = "black"
) +
# 補正したP値を治療条件毎に書き込む
add_pvalue(
data = condition_results,
xmin = "xmin",
xmax = "xmax",
label = "p {adjusted_p_value}",
y.position = 160, # P値を記載するY軸の高さの設定
textsize = 6,
bracket.color = "black"
)+
# ラベルの設定
labs(x = "治療条件", y = "LDL値", color = "育成条件", fill = "育成条件") +
# 見た目・レイアウトの調整
theme_classic()+
theme(
strip.background = element_blank(), # ファセットタイトルの背景を消す
strip.text = element_blank(), # ファセットタイトルのテキストを消す
axis.line = element_line(color = "black", size = 0.3, linetype = "solid"),
axis.text = element_text(color = "black", size = 12),
axis.title = element_text(size = 14),
axis.ticks.length = unit(-2, "mm"),
axis.ticks = element_line(color = "black", size = 0.3),
)




少し高度な内容だったのだ!



無料ソフトの限界やでな。もし楽したければGraphPadとかお金を出して使うのがええで。
まとめ
Two-way repeated measure ANOVAを用いた解析とグラフの描き方について例をお示ししました!
少しでもお役に立てたなら幸いです!!










コメント